Die offene, sehr
einfache Kernfrage lautet:
"
Endet die
Collatz-Folge für jede Eingabe bei der Eins? "
Die Antwort
ist ein klares Ja
!
- Trivial
und doch von entscheidender Bedeutung ist:
Es gibt 'abzählbar unendlich' viele Collatz-Folgen,
deren Verlauf bis zur 1 direkt gegeben ist. Die
betreffenden Startzahlen sind reine 2er Potenzen
n=2^i, mit
i>1
. Diese Folgen werden hier Collatz-Basisfolgen
genannt. Jede hat i
Schritte (Divisionen) und ist selbstverständlich nicht zyklisch (keine Schleife). Der letzte Schritt führt zwingend zu
der vorgegebenen EINS. Keine
dieser Folgen hat eine Collatz-Multiplikation.
- Es
ist leicht nachprüfbar, daß zu
jeder Collatz-Basisfolge eine große, bis sehr große Menge von
Collatz-Folgen gehört,
die alle die gleiche Länge i haben. Jede dieser Folgen hat
eine
bestimmte Anzahl m von Multiplikationen.
Bei obigem Link 'Neues bei Collatz'
wird im Detail gezeigt:
Aus
der Collatz-Basisfolge entstehen
durch gezielte Permutation (Ersatz und Tausch von Division u.
Multiplikation)
alle gleichlangen Collatz-Folgen.
Je
größer die Zahl der Multiplikationen, desto kleiner wird die
Startzahl n der Collatz-Folge.
Die Anwendung/Durchführung der Permutation ist in
verschiedener Weise möglich, z.B.
bei einem
Folgenaufbau von
rechts nach links, also beginnend bei dem Wert 1 .
•
In
der Literatur wird ein solches Vorgehen beschrieben
unter: Collatz-Graph.
• Denkbar ist auch, gezielt nur wenige Glieder einer (Basis-)
Folge
zu permutieren.
• Allg.: Immer wird der linke Teil einer Folge verändert, also ähnlich zu Collatz-Graph.
- Die
beste Permutation
ist der Normalfall,
nach Collatz. Es ist die Folgenentwicklung von links
nach
rechts, nach
gegebener Startzahl. Der sehr einfache
Collatz-Algorithmus ist eine perfekte Anweisung zur
Permutation der vorgegebenen Basisfolge. Vorgegeben bedeutet jedoch
nicht, die Folgenlänge
sei vorgegeben oder vorhersagbar!
Das
normale Verfahren 'ab Startzahl' hat den Vorteil, daß
während des Folgenaufbaues die zunächst unbekannte
Folgenlänge unbegrenzt verlängert wird. Dies geschieht ohne Einwirkung auf das
konstante Folgenende mit "...16,8,4,2,1".
Die letzten 4 Schritte werden niemals permutiert, denn das iterative
Verfahren bzw. die Permutation bricht ab,
wenn die Collatz-Folge in reine 2er
Potenzen übergeht, das ist spätestens mit der Zahl 16 der Fall... 16
mod 3=1.
Insgesamt werden i Schritte ausgeführt. Damit steht am Ende fest, zu
welcher Basisfolge n=2^i
die aktuelle Folge gehört. Für die endliche Gliederzahl i
existiert keine
Obergrenze.
- Die
korrekte Form eines Beweises ist schwierig. Mir ist nicht
bekannt, wie
in der Kombinatorik vorzugehen wäre. Ich gehe davon aus,
daß die unten gegebene Darstellung der Permutationan
einer
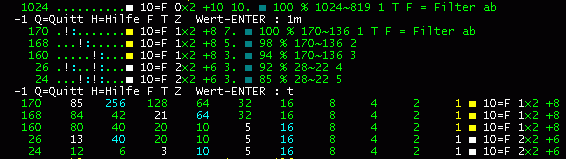
Basisfolge i=2^10=1024
den Anforderungen genügt. Ein
Übergang auf 2^i, in der Art einer vollständigen
Induktion, sollte dem Fachmann möglich
sein.
Klar beantwortet ist:
Jede Collatz-Folge
endet mit dem trivialen Ende
aller Collatz-Basisfolgen n=2^i. Dieses
Ende ist die EINS, auch
dann, wenn die Anzahl der endlichen Schritte i gegen 'abzählbar
unendlich' geht.
- Plausibilität
Unter Die komprimierte
Collatz-Folge wird gezeigt, daß jede Collatz-Folge für
eine gegebene Zahl n eindeutig
ist, da ihr Verlauf durch die Primfaktoren von n+1, n'+1 ...
bestimmt wird. Das bedeutet aber auch: Der Folgenverlauf ist
ohne fortgesetzte Primfaktorenanalyse von n+1 nicht vorhersagbar
!!!
Es bestätigte sich der mittlere
Verkleinerungsfaktor pro Folgenschritt von ~3/4. Es
ist richtig, daß dieses Merkmal alleine nicht als Beweis für
die EINS
dienen
kann, wegen der alten Befürchtung:
"Es kann nicht ausgeschlossen werden , daß
die Multiplikationen die Divisionen
überwiegen."
Das ist eindeutig widerlegt, denn nur die Primfaktoren von n+1
bestimmen
den Folgenverlauf. Damit
ist bekannt, bei welchen Folgen die maximale,
endliche Anzahl
von Collatz-
Multiplikationen auftritt. Es sind die Folgen der Mersenne-Zahlen,
mit i Multiplikationen nach Collatz. Siehe nächsten
Punkt. Örtlich
können die Folgenwerte durch Multiplikationen deutlich steigen. Es wäre
aber falsch, daraus
abzuleiten, daß sie endlos ansteigen können. Eine Folge
kann eventuell sehr lang werden. Mit steigendem i und jedem neuen Glied
n bestimmen neue Primfaktoren von n+1 den weiteren Verlauf.
Nach bestätigter Theorie - mittlerer Faktor ~3/4 - werden die
Werte jeder Folge im
Mittel fortlaufend kleiner...
und
gehen über zu kleineren 2er Potenzen und letztlich zu 2^0 =
1.
- Zu
Mersenne-Zahlen:
Die Collatz-Folge jeder
Mersenne-Zahl
2^i -1 beginnt
mit einer endlichen Maximalzahl von i
Collatz-Multiplikationen, an
die sich sofort eine Vielzahl wechselnder Operationen anschließt. Damit
kann man gezielt z.B. 6000 Collatz-Multiplikationen erzeugen,
ohne daß es zu einem Überlauf kommt. Natürlich ergibt das eine neue,
sehr
lange
Folge, doch diese endet wieder - über weitere Permutationen - bei der
gegebenen EINS aller Basisfolgen !!!
Siehe:
Extreme Collatz-Folge zu
n= 2^6000 -1
- Allgemein gilt
ein Beweis
als erbracht, wenn es zu einer Vermutung kein Gegenbeispiel gibt, bzw.
nicht geben kann. Ein solcher Beweis ist leicht zu führen:
Ein
konkretes Gegenbeispiel wäre eine 'unendlich' lange, beliebig aufgebaute
Collatz-Folge, die
nicht bei 1 endet. Die Folge hätte dann eine zugehörige, ebenfalls
'unendlich' lange Basisfolge. Diese kann es aber im Bereich der
natürlichen Zahlen definitionsgemäß nicht geben. Basisfolge und
Normalfolge (nach Collatz) bedingen sich gegenseitig. Zu jeder
endlichen Basisfolge 2^i (i bis 'abzählbar unendlich') gibt es
gleichlange, durch Permutation ableitbare Collatz-Folgen. Sie haben eine
Startzahl
<2^i und sie haben das durch die Basisfolge vorgegebene, nicht permutierte Ende
bei 1.
|