Bisher
fehlt ein Beweis
dafür, daß der Collatz-Algorithmus immer zur EINS führt.
Mit hohem Computeraufwand wurde und wird vergeblich nach einem Gegenbeispiel gesucht.
Tatsächlich läßt sich bereits mit einfachen Mitteln zeigen, daß der Weg zur Collatz-EINS
in unserem Zahlensystem - besser im Dualsystem - fest verankert ist.
Formale Beweise sind die zweite Seite der Medaille, gewonnene Erkenntnisse die erste!
Die Lösung des Problems steht und fällt mit der richtigen Fragestellung. Sie lautet:
Wodurch entstehen Collatz-Folgen gleicher Länge ? Durch Permutation !
Häufig wird die Folge der Zahl n=27 besprochen. Sie sei besonders lang, insbesondere im Hinblick auf die benachbarten, kürzeren Collatz-Folgen. Die ungekürzte 27er Folge führt nach i=111 Schritten zur EINS. Von diesen 111 Schritten sind m=41 Multiplikationen. ( Die sogenannte 'gekürzte' Folge hat nur 70 Schritte, da man die erste Division nach einer Multiplikation in letztere einschließt und nicht mitzählt. )
An der Folge der Zahl 27 möchte ich die Zusammenhänge erläutern:
Link zu
'Collatz-Folgen': An anderer Stelle dieser
Homepage nannte ich bereits...
Primzahlen oder die Magie der Zahlen http://euroware.de von Reinhold Kiebart
Auch das hier behandelte Thema finden Sie dort in einer brillanten Präsentation, mit
einem superschnellem Suchprogramm in einer Windowsprogrammierung unter KK.exe.
Mit hohem Computeraufwand wurde und wird vergeblich nach einem Gegenbeispiel gesucht.
Tatsächlich läßt sich bereits mit einfachen Mitteln zeigen, daß der Weg zur Collatz-EINS
in unserem Zahlensystem - besser im Dualsystem - fest verankert ist.
Formale Beweise sind die zweite Seite der Medaille, gewonnene Erkenntnisse die erste!
Die Lösung des Problems steht und fällt mit der richtigen Fragestellung. Sie lautet:
Wodurch entstehen Collatz-Folgen gleicher Länge ? Durch Permutation !
Häufig wird die Folge der Zahl n=27 besprochen. Sie sei besonders lang, insbesondere im Hinblick auf die benachbarten, kürzeren Collatz-Folgen. Die ungekürzte 27er Folge führt nach i=111 Schritten zur EINS. Von diesen 111 Schritten sind m=41 Multiplikationen. ( Die sogenannte 'gekürzte' Folge hat nur 70 Schritte, da man die erste Division nach einer Multiplikation in letztere einschließt und nicht mitzählt. )
An der Folge der Zahl 27 möchte ich die Zusammenhänge erläutern:
n
= 2^i = 2^111 = 2596.148429.267413.814265.248164.610048
Das sind 34 Dezimalstellen, nach je 6 Stellen steht ein Millionen-Punkt.
Das sind 34 Dezimalstellen, nach je 6 Stellen steht ein Millionen-Punkt.
Jeder
Schüler, dem Potenzen
bekannt sind, sollte zu der hohen Zahl die Collatz-Folge
anschreiben können.
Es sind 111 Operationen (Divisionen durch 2), die sicher zu
dem Ziel 1 führen. Eine
Collatz-Multiplikation
tritt dabei nicht auf.
Was verbindet die 27er Folge und die 34 stelligen Zahl? Beide Folgen sind gleich lang. Die Folge 2^111 ist die höchstgelegene Folge mit 111 Gliedern. Die 27er Folge liegt dagegen schon nahe der Null. Zwischen diesen beiden Zahlen liegen tausende von Folgen gleicher Länge aber mit unterschiedlich vielen Multiplikationen. Ein klassisches Suchprogramm, das Folge für Folge auf die Anzahl ihrer Glieder testen würde, ist zum Scheitern verurteilt, wegen der hohen Stellenzahl mit entsprechend sehr großen Lücken zwischen den betreffenden Folgen. Neue Erkenntmisse gestatten jedoch, den Ort auf der Zahlengeraden recht genau abzuschätzen. Zusätzlich optimierte Suchroutinen, siehe Link ganz unten, liefern ein schnelles Ergebnis.
Setzt man die gezeigte Abschätzung auf das Beispiel n=2^111 an, findet man die 2 tiefstgelegenen Orte, an denen Folgen mit 111 Schritten und 40 bzw. 41 Multiplikationen zu erwarten sind:
2^111/6^40 ~194 bis ~155 (80%) und 2^111/6^41 ~32 bis ~25
Das nächste Folgenbild zeigt diese Kalkulation mit der magenta Markierung ======= .
Zeile 166 (bis 164) und 27.... Geradezu primitiv ist: 166 div 6 = 27 !!!
Zu folgenden Bildern: Punkte sind Divisionen, Rufzeichen sind Multiplikationen gekürzter Folgen.
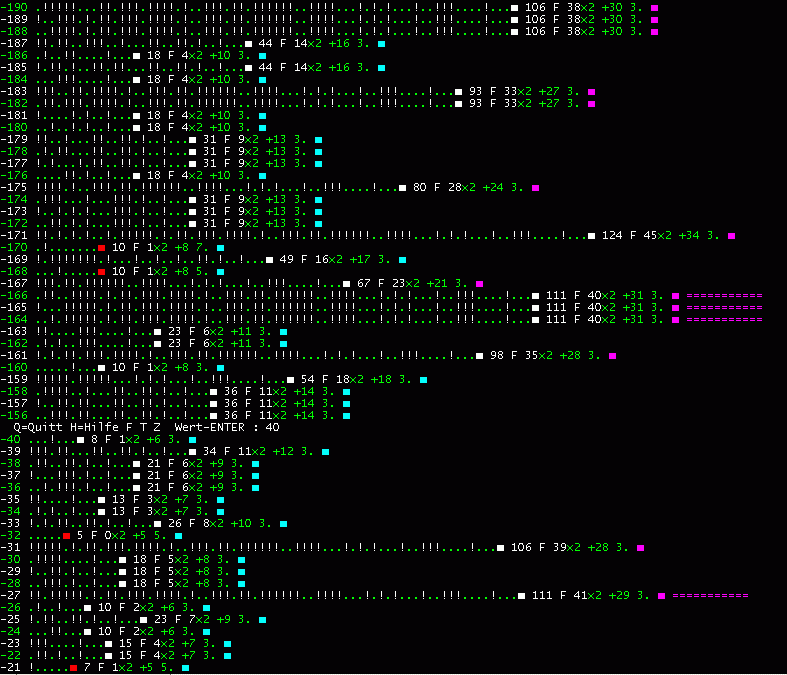
Frage: Nach welchem Prinzip sind die 1 bis max. 41 Multiplikationen innerhalb der 70 bzw. 111 Glieder verteilt? ... Sie sind kombinatorisch so verteilt, daß bei jedem Schritt die Collatz-Vorschrift eingehalten wird. In der Kombinatorik verwendet man den Begriff 'Permutation'. Hier soll darunter verstanden werden: Das Vertauschen oder Ersetzen von Gliedern einer Folge. Der gezielte Tausch von Divisionen in eine Multiplikation kann - in Richtung der Folge - nur vor Zahlen erfolgen, die mod 3 den Rest 1 liefern. Oberhalb der 4 ist 16 die kleinste dieser Zahlen.
Das Bauprinzip der Folgen läßt sich an einer kleineren Zahl wie 2^16 etwas übersichtlicher zeigen,
wobei dieser Aufbau bis 'abzählbar unendlich' gegeben ist. Es gibt keine Obergrenze für 2^i !
Bei der absteigenden Anzeige gleichlanger Folgen mit Symbolen erkennt man eine bemerkenswerte Systematik. Es entstehen regelmäßige Muster durch Permutation, jeweils innerhalb der Anzahl von gleichvielen Multiplikationen zwischen den dualen Divisionen.
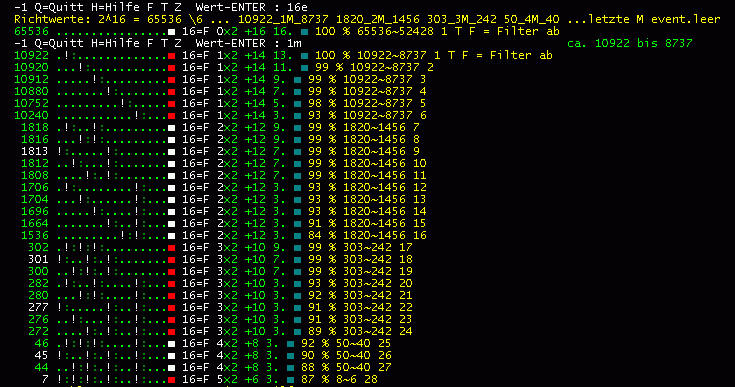
... oberes Bild: alle Folgen zu 2^16, mit Symbolen
unteres Bild: die gleichen Folgen mit Zahlen ....
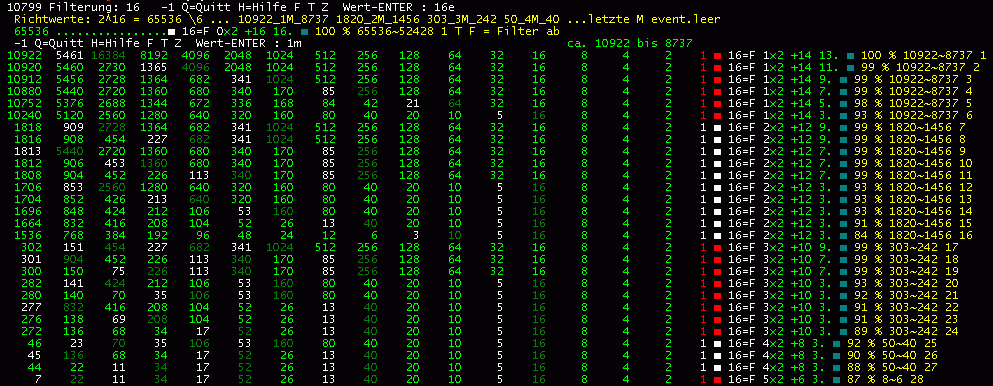
Die 28 Zeilen (+1) zeigen alle ungekürzten Collatz-Folgen mit i=16 Schritten
und m ... Multiplikationen.
Block m=0 2^16 = 65536 (1 Zahl) Kalkulation
Block m=1 10922 bis 10240 10922 - 8737
Block m=2 1818 - 1536 1820 - 1456
Block m=3 302 - 272 303 - 242
Block m=4 46 - 44 50 - 40
Block m=5 7 ... nur eine Zahl 8 - 6
Die Permutationsregeln stellen sicher, daß die Endwerte aller Basisfolgen von n=2^i, das sind die Potenzen 16,8,4,2,1 erhalten bleiben. Unendlich viele Gruppen gleich langer Collatz-Folgen erreichen auf diese Weise die immanente EINS des Dualsystems.
Die wichtigste Permutationsregel ist: In einer Collatz-Folge darf - rückwärts gelesen - ein Multiplikationsschritt nur auf eine Zahl folgen, die mod 3 Rest 1 hat... eben nach Collatz.
Mit Mitteln der Kombinatorik sollte es möglich sein, den aufgezeigten Zusammenhang und den Weg zur Collatz-EINS besser zu beschreiben. Die Antwort auf das scheinbar offene Collatz-Problem ist fest verankert in den bestimmenden Dualzahlen, ausgehend von den Collatz-Basisfolgen. Genau dazu sehen Sie bitte den letzten Ausdruck unten... Beispiel n = 2^23
Totale zu Collatz /...Link dazu siehe ganz unten
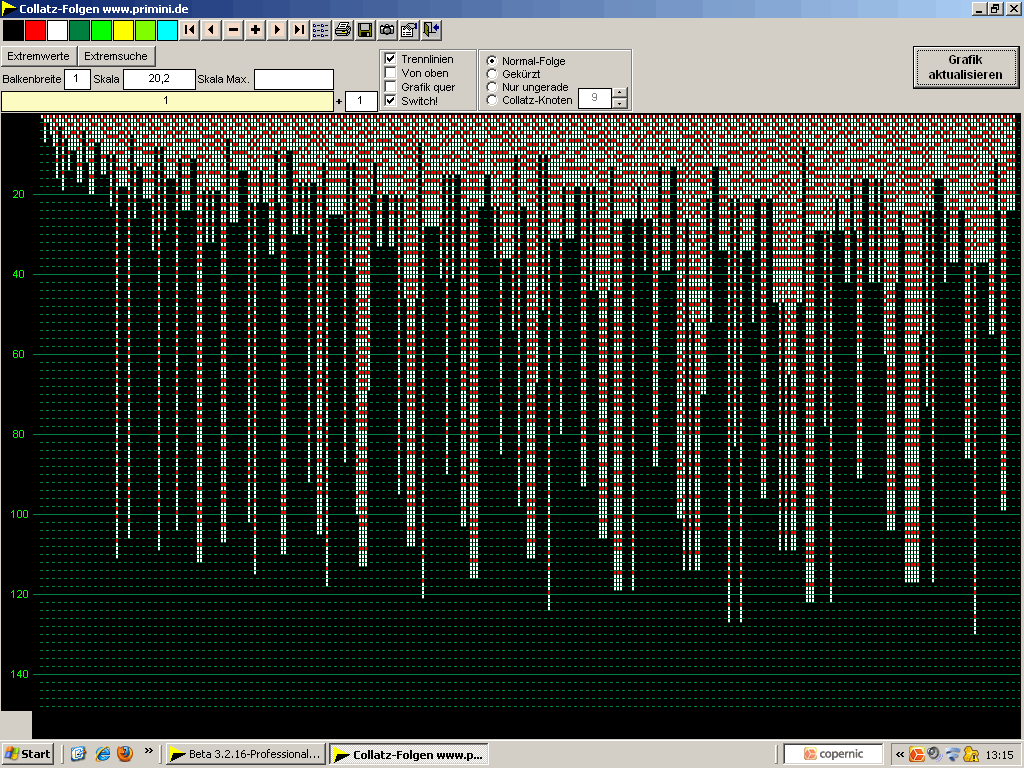
Diese an sich unübliche Darstellung gibt die strenge Collatz-Systematik besonders gut wieder. Die weißen Marken kennzeichnen die Folgen aller natürlichen Zahlen. Die Marken liegen gezielt auf blauen Balken, den möglichen Orten auf der Zahlengeraden (Bereich ~80 bis 100%, siehe oben).
Auf den Balken liegen jeweils Folgen mit gleichvielen Collatz-Multiplikationen.
Die senkrechte x Linie markiert eine beliebige Folge (im Original mit Kreis+Mauspfeil). Nur an einem Schnittpunkt der Linie mit einem blauen Balken, z.B. Zeile 34, kann und muß eine Collatz-Folge liegen.
Nachträglich eingetragene Zahlen, türkis: Anzahl der Multiplikationen m
Y-Achse: i Länge der Folgen
X-Achse: n Ordnungszahl der Collatz-Folgen, hier von 1 bis nahe 1000
Tooltip ganz unten: n=229 i.m = 34.10 ... Folgenlänge.Multiplikationen
(k) = kurz oder gekürzte Folge 34-10 = 24 Zeichen
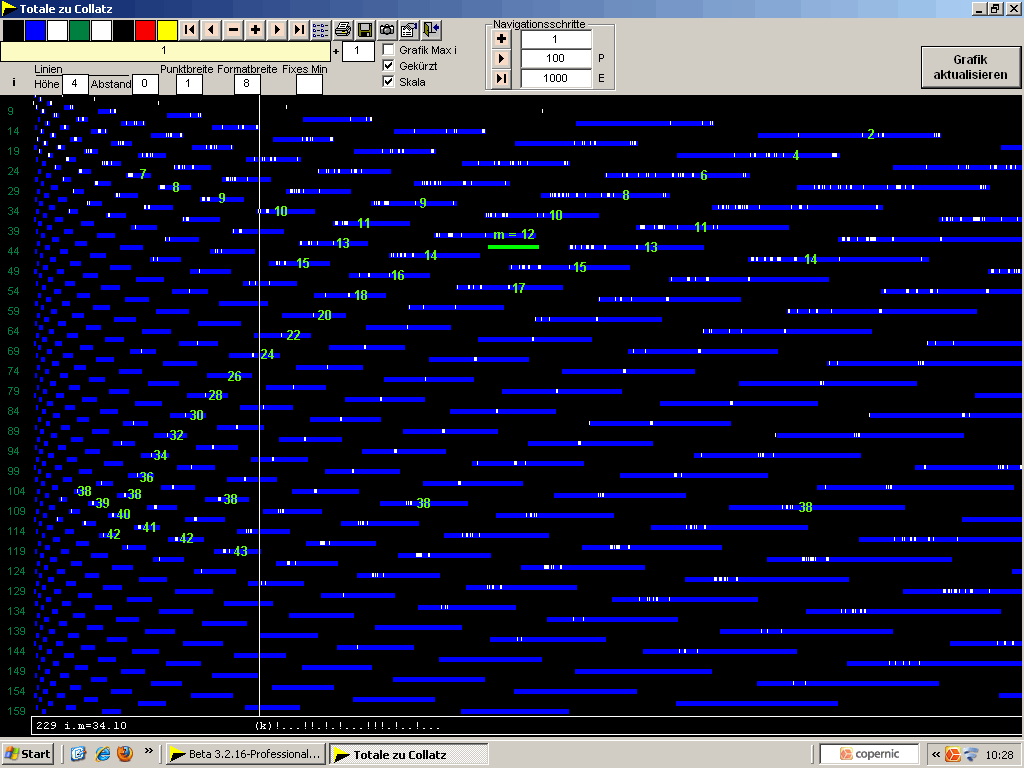
... Und wenn Sie genau hinsehen, werden Sie feststellen: Die nächste Collatz-Grafik zeigt die gleichen Daten wie oben - nur in einer anderen Aufbereitung.
Studieren Sie bitte genau:
'Synchroner Verlauf' der Collatz-Folgen und der Dualzahlen von n, insbesondere in Block 1 (und 2), also bei m=1 (und m=2). Ab Block 3 oder 4 (m=3 oder 4 Multiplikationen) sind die vorhandenen Permutationsregeln mit dem Auge kaum noch zu erfassen. Die Tausch-Systematik und die Anlehnung an Dualzahlen besteht jedoch in gleicher Weise wie in Block 1 und 2.
n = 2^20 Collatz-Folge ... aus KK.exe
▼ (ungekürzt) Anzahl Multiplikationen
Block 0: ▼ ▼ duale Darstellung von n
Zahl n Glieder = i.m ▼
1.048.576 .................... 20.0 !.................... statt 100000000000000000000
oben: 1 Folge mit 0 Multiplikationen
Block 1: (1 Multiplikation)
174.762 .!.................. 20.1 !.!.!.!.!.!.!.!.!. statt 101010101010101010
174.760 ...!................ 20.1 !.!.!.!.!.!.!.!... 101010101010101000
174.752 .....!.............. 20.1 !.!.!.!.!.!.!..... 101010101010100000
174.720 .......!............ 20.1 !.!.!.!.!.!....... usw.
174.592 .........!.......... 20.1 !.!.!.!.!.........
174.080 ...........!........ 20.1 !.!.!.!...........
172.032 .............!...... 20.1 !.!.!.............
163.840 ...............!.... 20.1 !.!...............
oben: 8 Folgen mit 1 Multiplikation
Block 2:
29.126 .!.!................ 20.2 !!!...!!!...!!.
29.125 !....!.............. 20.2 !!!...!!!...!.!
29.124 ..!..!.............. 20.2 !!!...!!!...!..
29.098 .!.......!.......... 20.2 !!!...!!.!.!.!.
29.096 ...!.....!.......... 20.2 !!!...!!.!.!...
29.088 .....!...!.......... 20.2 !!!...!!.!.....
29.056 .......!.!.......... 20.2 !!!...!!.......
29.013 !..........!........ 20.2 !!!...!.!.!.!.!
29.012 ..!........!........ 20.2 !!!...!.!.!.!..
29.008 ....!......!........ 20.2 !!!...!.!.!....
28.992 ......!....!........ 20.2 !!!...!.!......
28.928 ........!..!........ 20.2 !!!...!........
27.306 .!.............!.... 20.2 !!.!.!.!.!.!.!.
27.304 ...!...........!.... 20.2 !!.!.!.!.!.!...
27.296 .....!.........!.... 20.2 !!.!.!.!.!.....
27.264 .......!.......!.... 20.2 !!.!.!.!.......
27.136 .........!.....!.... 20.2 !!.!.!.........
26.624 ...........!...!.... 20.2 !!.!...........
24.576 .............!.!.... 20.2 !!.............
oben: 19 Folgen mit 2 Multiplikationen
4.849 !..!.....!.......... 20.3 !..!.!!!!...!
4.842 .!.....!.!.......... 20.3 !..!.!!!.!.!.
4.840 ...!...!.!.......... 20.3 !..!.!!!.!...
4.835 !.!........!........ 20.3 !..!.!!!...!!
4.834 .!..!......!........ 20.3 !..!.!!!...!.
4.832 .....!.!.!.......... 20.3 !..!.!!!.....
4.821 !.......!..!........ 20.3 !..!.!!.!.!.!
4.820 ..!.....!..!........ 20.3 !..!.!!.!.!..
4.816 ....!...!..!........ 20.3 !..!.!!.!....
4.800 ......!.!..!........ 20.3 !..!.!!......
4.550 .!.!...........!.... 20.3 !...!!!...!!.
4.549 !....!.........!.... 20.3 !...!!!...!.!
4.548 ..!..!.........!.... 20.3 !...!!!...!..
4.522 .!.......!.....!.... 20.3 !...!!.!.!.!.
4.520 ...!.....!.....!.... 20.3 !...!!.!.!...
4.512 .....!...!.....!.... 20.3 !...!!.!.....
4.480 .......!.!.....!.... 20.3 !...!!.......
4.437 !..........!...!.... 20.3 !...!.!.!.!.!
4.436 ..!........!...!.... 20.3 !...!.!.!.!..
4.432 ....!......!...!.... 20.3 !...!.!.!....
4.416 ......!....!...!.... 20.3 !...!.!......
4.352 ........!..!...!.... 20.3 !...!........
oben: 22 Folgen mit 3 Multiplikationen
806 .!.!...!.!.......... 20.4 !!..!..!!.
805 !....!.!.!.......... 20.4 !!..!..!.!
804 ..!..!.!.!.......... 20.4 !!..!..!..
803 !.!.....!..!........ 20.4 !!..!...!!
802 .!..!...!..!........ 20.4 !!..!...!.
753 !..!.....!.....!.... 20.4 !.!!!!...!
746 .!.....!.!.....!.... 20.4 !.!!!.!.!.
744 ...!...!.!.....!.... 20.4 !.!!!.!...
739 !.!........!...!.... 20.4 !.!!!...!!
738 .!..!......!...!.... 20.4 !.!!!...!.
736 .....!.!.!.....!.... 20.4 !.!!!.....
725 !.......!..!...!.... 20.4 !.!!.!.!.!
724 ..!.....!..!...!.... 20.4 !.!!.!.!..
720 ....!...!..!...!.... 20.4 !.!!.!....
704 ......!.!..!...!.... 20.4 !.!!......
oben: 15 Folgen mit 4 Multiplikationen
122 .!...!.!.!.....!.... 20.5 !!!!.!.
120 ...!.!.!.!.....!.... 20.5 !!!!...
117 !.....!.!..!...!.... 20.5 !!!.!.!
116 ..!...!.!..!...!.... 20.5 !!!.!..
112 ....!.!.!..!...!.... 20.5 !!!....
oben: 5 Folgen mit 5 Multiplikationen
19 !.!...!.!..!...!.... 20.6 !..!!
18 .!..!.!.!..!...!.... 20.6 !..!.
oben: 2 Folgen mit 6 Multiplikationen im niedrigsten Block
Die nächste Darstellung i=23 hat gegen oben eine andere Sortierung der Spalten !!
Bitte beachten Sie den symmetrischen Verlauf:
Dualzahlen links und Collatz-Folge rechts (Ausdruck von KK.exe)
! = 1 . = 0 ! = Multiplikation . = Division
n = 2^23 Permutation der ungekürzten
i m Dualzahl zu n Collatz-Folge zu Zahl n
23.00 !....................... ....................... 8388608 Diff.:
23.01 !.!.!.!.!.!.!.!.!.!.! !...................... 1398101 0
23.01 !.!.!.!.!.!.!.!.!.!.. ..!.................... 1398100 1
23.01 !.!.!.!.!.!.!.!.!.... ....!.................. 1398096 4
23.01 !.!.!.!.!.!.!.!...... ......!................ 1398080 16
23.01 !.!.!.!.!.!.!........ ........!.............. 1398016 64
23.01 !.!.!.!.!.!.......... ..........!............ 1397760 256
23.01 !.!.!.!.!............ ............!.......... 1396736 1024
23.01 !.!.!.!.............. ..............!........ 1392640 4096
23.01 !.!.!................ ................!...... 1376256 16384
23.01 !.!.................. ..................!.... 1310720 65536
oberer Block jede Zeile 1 Multiplikation nach Collatz
unterer Block jede Zeile 2 Multiplikationen :
23.02 !!!...!!!...!!.!.! !.....!................ 233013
23.02 !!!...!!!...!!.!.. ..!...!................ 233012
23.02 !!!...!!!...!!.... ....!.!................ 233008
23.02 !!!...!!!...!.!.!. .!......!.............. 233002
23.02 !!!...!!!...!.!... ...!....!.............. 233000
23.02 !!!...!!!...!..... .....!..!.............. 232992
23.02 !!!...!!.!.!.!.!.! !...........!.......... 232789
23.02 !!!...!!.!.!.!.!.. ..!.........!.......... 232788
23.02 !!!...!!.!.!.!.... ....!.......!.......... 232784
23.02 !!!...!!.!.!...... ......!.....!.......... 232768
23.02 !!!...!!.!........ ........!...!.......... 232704
23.02 !!!...!!.......... ..........!.!.......... 232448
23.02 !!!...!.!.!.!.!.!. .!............!........ 232106
23.02 !!!...!.!.!.!.!... ...!..........!........ 232104
23.02 !!!...!.!.!.!..... .....!........!........ 232096
23.02 !!!...!.!.!....... .......!......!........ 232064
23.02 !!!...!.!......... .........!....!........ 231936
23.02 !!!...!........... ...........!..!........ 231424
23.02 !!.!.!.!.!.!.!.!.! !.................!.... 218453
23.02 !!.!.!.!.!.!.!.!.. ..!...............!.... 218452
23.02 !!.!.!.!.!.!.!.... ....!.............!.... 218448
23.02 !!.!.!.!.!.!...... ......!...........!.... 218432
23.02 !!.!.!.!.!........ ........!.........!.... 218368
23.02 !!.!.!.!.......... ..........!.......!.... 218112
23.02 !!.!.!............ ............!.....!.... 217088
23.02 !!.!.............. ..............!...!.... 212992
23.02 !!................ ................!.!.... 196608
usw. bis zur kleinsten Folge mit 7 Multiplikationen:
23.07 !!..! !..!.!...!.!..!...!.... n = 25
Lieber Leser, wenn Sie bis hierher gekommen sind, dann gibt es trotzdem kein Verdienstkreuz.
Aber es gibt die versteckte Freude an der Symmetrie von Dualzahlen und Collatz-Folgen. Und:
Der Hintergrund für den Beweis der Collatz-EINS sollte klar geworden sein !!
Was verbindet die 27er Folge und die 34 stelligen Zahl? Beide Folgen sind gleich lang. Die Folge 2^111 ist die höchstgelegene Folge mit 111 Gliedern. Die 27er Folge liegt dagegen schon nahe der Null. Zwischen diesen beiden Zahlen liegen tausende von Folgen gleicher Länge aber mit unterschiedlich vielen Multiplikationen. Ein klassisches Suchprogramm, das Folge für Folge auf die Anzahl ihrer Glieder testen würde, ist zum Scheitern verurteilt, wegen der hohen Stellenzahl mit entsprechend sehr großen Lücken zwischen den betreffenden Folgen. Neue Erkenntmisse gestatten jedoch, den Ort auf der Zahlengeraden recht genau abzuschätzen. Zusätzlich optimierte Suchroutinen, siehe Link ganz unten, liefern ein schnelles Ergebnis.
|
Setzt man die gezeigte Abschätzung auf das Beispiel n=2^111 an, findet man die 2 tiefstgelegenen Orte, an denen Folgen mit 111 Schritten und 40 bzw. 41 Multiplikationen zu erwarten sind:
2^111/6^40 ~194 bis ~155 (80%) und 2^111/6^41 ~32 bis ~25
Das nächste Folgenbild zeigt diese Kalkulation mit der magenta Markierung ======= .
Zeile 166 (bis 164) und 27.... Geradezu primitiv ist: 166 div 6 = 27 !!!
Zu folgenden Bildern: Punkte sind Divisionen, Rufzeichen sind Multiplikationen gekürzter Folgen.

Frage: Nach welchem Prinzip sind die 1 bis max. 41 Multiplikationen innerhalb der 70 bzw. 111 Glieder verteilt? ... Sie sind kombinatorisch so verteilt, daß bei jedem Schritt die Collatz-Vorschrift eingehalten wird. In der Kombinatorik verwendet man den Begriff 'Permutation'. Hier soll darunter verstanden werden: Das Vertauschen oder Ersetzen von Gliedern einer Folge. Der gezielte Tausch von Divisionen in eine Multiplikation kann - in Richtung der Folge - nur vor Zahlen erfolgen, die mod 3 den Rest 1 liefern. Oberhalb der 4 ist 16 die kleinste dieser Zahlen.
Das Bauprinzip der Folgen läßt sich an einer kleineren Zahl wie 2^16 etwas übersichtlicher zeigen,
wobei dieser Aufbau bis 'abzählbar unendlich' gegeben ist. Es gibt keine Obergrenze für 2^i !
Bei der absteigenden Anzeige gleichlanger Folgen mit Symbolen erkennt man eine bemerkenswerte Systematik. Es entstehen regelmäßige Muster durch Permutation, jeweils innerhalb der Anzahl von gleichvielen Multiplikationen zwischen den dualen Divisionen.

... oberes Bild: alle Folgen zu 2^16, mit Symbolen
unteres Bild: die gleichen Folgen mit Zahlen ....

Die 28 Zeilen (+1) zeigen alle ungekürzten Collatz-Folgen mit i=16 Schritten
und m ... Multiplikationen.
Block m=0 2^16 = 65536 (1 Zahl) Kalkulation
Block m=1 10922 bis 10240 10922 - 8737
Block m=2 1818 - 1536 1820 - 1456
Block m=3 302 - 272 303 - 242
Block m=4 46 - 44 50 - 40
Block m=5 7 ... nur eine Zahl 8 - 6
Die Permutationsregeln stellen sicher, daß die Endwerte aller Basisfolgen von n=2^i, das sind die Potenzen 16,8,4,2,1 erhalten bleiben. Unendlich viele Gruppen gleich langer Collatz-Folgen erreichen auf diese Weise die immanente EINS des Dualsystems.
Die wichtigste Permutationsregel ist: In einer Collatz-Folge darf - rückwärts gelesen - ein Multiplikationsschritt nur auf eine Zahl folgen, die mod 3 Rest 1 hat... eben nach Collatz.
| Resümee
|
Mit Mitteln der Kombinatorik sollte es möglich sein, den aufgezeigten Zusammenhang und den Weg zur Collatz-EINS besser zu beschreiben. Die Antwort auf das scheinbar offene Collatz-Problem ist fest verankert in den bestimmenden Dualzahlen, ausgehend von den Collatz-Basisfolgen. Genau dazu sehen Sie bitte den letzten Ausdruck unten... Beispiel n = 2^23
Totale zu Collatz /...Link dazu siehe ganz unten
Diese an sich unübliche Darstellung gibt die strenge Collatz-Systematik besonders gut wieder. Die weißen Marken kennzeichnen die Folgen aller natürlichen Zahlen. Die Marken liegen gezielt auf blauen Balken, den möglichen Orten auf der Zahlengeraden (Bereich ~80 bis 100%, siehe oben).
Auf den Balken liegen jeweils Folgen mit gleichvielen Collatz-Multiplikationen.
Die senkrechte x Linie markiert eine beliebige Folge (im Original mit Kreis+Mauspfeil). Nur an einem Schnittpunkt der Linie mit einem blauen Balken, z.B. Zeile 34, kann und muß eine Collatz-Folge liegen.
Nachträglich eingetragene Zahlen, türkis: Anzahl der Multiplikationen m
Y-Achse: i Länge der Folgen
X-Achse: n Ordnungszahl der Collatz-Folgen, hier von 1 bis nahe 1000
Tooltip ganz unten: n=229 i.m = 34.10 ... Folgenlänge.Multiplikationen
(k) = kurz oder gekürzte Folge 34-10 = 24 Zeichen

... Und wenn Sie genau hinsehen, werden Sie feststellen: Die nächste Collatz-Grafik zeigt die gleichen Daten wie oben - nur in einer anderen Aufbereitung.

Studieren Sie bitte genau:
'Synchroner Verlauf' der Collatz-Folgen und der Dualzahlen von n, insbesondere in Block 1 (und 2), also bei m=1 (und m=2). Ab Block 3 oder 4 (m=3 oder 4 Multiplikationen) sind die vorhandenen Permutationsregeln mit dem Auge kaum noch zu erfassen. Die Tausch-Systematik und die Anlehnung an Dualzahlen besteht jedoch in gleicher Weise wie in Block 1 und 2.
n = 2^20 Collatz-Folge ... aus KK.exe
▼ (ungekürzt) Anzahl Multiplikationen
Block 0: ▼ ▼ duale Darstellung von n
Zahl n Glieder = i.m ▼
1.048.576 .................... 20.0 !.................... statt 100000000000000000000
oben: 1 Folge mit 0 Multiplikationen
Block 1: (1 Multiplikation)
174.762 .!.................. 20.1 !.!.!.!.!.!.!.!.!. statt 101010101010101010
174.760 ...!................ 20.1 !.!.!.!.!.!.!.!... 101010101010101000
174.752 .....!.............. 20.1 !.!.!.!.!.!.!..... 101010101010100000
174.720 .......!............ 20.1 !.!.!.!.!.!....... usw.
174.592 .........!.......... 20.1 !.!.!.!.!.........
174.080 ...........!........ 20.1 !.!.!.!...........
172.032 .............!...... 20.1 !.!.!.............
163.840 ...............!.... 20.1 !.!...............
oben: 8 Folgen mit 1 Multiplikation
Block 2:
29.126 .!.!................ 20.2 !!!...!!!...!!.
29.125 !....!.............. 20.2 !!!...!!!...!.!
29.124 ..!..!.............. 20.2 !!!...!!!...!..
29.098 .!.......!.......... 20.2 !!!...!!.!.!.!.
29.096 ...!.....!.......... 20.2 !!!...!!.!.!...
29.088 .....!...!.......... 20.2 !!!...!!.!.....
29.056 .......!.!.......... 20.2 !!!...!!.......
29.013 !..........!........ 20.2 !!!...!.!.!.!.!
29.012 ..!........!........ 20.2 !!!...!.!.!.!..
29.008 ....!......!........ 20.2 !!!...!.!.!....
28.992 ......!....!........ 20.2 !!!...!.!......
28.928 ........!..!........ 20.2 !!!...!........
27.306 .!.............!.... 20.2 !!.!.!.!.!.!.!.
27.304 ...!...........!.... 20.2 !!.!.!.!.!.!...
27.296 .....!.........!.... 20.2 !!.!.!.!.!.....
27.264 .......!.......!.... 20.2 !!.!.!.!.......
27.136 .........!.....!.... 20.2 !!.!.!.........
26.624 ...........!...!.... 20.2 !!.!...........
24.576 .............!.!.... 20.2 !!.............
oben: 19 Folgen mit 2 Multiplikationen
4.849 !..!.....!.......... 20.3 !..!.!!!!...!
4.842 .!.....!.!.......... 20.3 !..!.!!!.!.!.
4.840 ...!...!.!.......... 20.3 !..!.!!!.!...
4.835 !.!........!........ 20.3 !..!.!!!...!!
4.834 .!..!......!........ 20.3 !..!.!!!...!.
4.832 .....!.!.!.......... 20.3 !..!.!!!.....
4.821 !.......!..!........ 20.3 !..!.!!.!.!.!
4.820 ..!.....!..!........ 20.3 !..!.!!.!.!..
4.816 ....!...!..!........ 20.3 !..!.!!.!....
4.800 ......!.!..!........ 20.3 !..!.!!......
4.550 .!.!...........!.... 20.3 !...!!!...!!.
4.549 !....!.........!.... 20.3 !...!!!...!.!
4.548 ..!..!.........!.... 20.3 !...!!!...!..
4.522 .!.......!.....!.... 20.3 !...!!.!.!.!.
4.520 ...!.....!.....!.... 20.3 !...!!.!.!...
4.512 .....!...!.....!.... 20.3 !...!!.!.....
4.480 .......!.!.....!.... 20.3 !...!!.......
4.437 !..........!...!.... 20.3 !...!.!.!.!.!
4.436 ..!........!...!.... 20.3 !...!.!.!.!..
4.432 ....!......!...!.... 20.3 !...!.!.!....
4.416 ......!....!...!.... 20.3 !...!.!......
4.352 ........!..!...!.... 20.3 !...!........
oben: 22 Folgen mit 3 Multiplikationen
806 .!.!...!.!.......... 20.4 !!..!..!!.
805 !....!.!.!.......... 20.4 !!..!..!.!
804 ..!..!.!.!.......... 20.4 !!..!..!..
803 !.!.....!..!........ 20.4 !!..!...!!
802 .!..!...!..!........ 20.4 !!..!...!.
753 !..!.....!.....!.... 20.4 !.!!!!...!
746 .!.....!.!.....!.... 20.4 !.!!!.!.!.
744 ...!...!.!.....!.... 20.4 !.!!!.!...
739 !.!........!...!.... 20.4 !.!!!...!!
738 .!..!......!...!.... 20.4 !.!!!...!.
736 .....!.!.!.....!.... 20.4 !.!!!.....
725 !.......!..!...!.... 20.4 !.!!.!.!.!
724 ..!.....!..!...!.... 20.4 !.!!.!.!..
720 ....!...!..!...!.... 20.4 !.!!.!....
704 ......!.!..!...!.... 20.4 !.!!......
oben: 15 Folgen mit 4 Multiplikationen
122 .!...!.!.!.....!.... 20.5 !!!!.!.
120 ...!.!.!.!.....!.... 20.5 !!!!...
117 !.....!.!..!...!.... 20.5 !!!.!.!
116 ..!...!.!..!...!.... 20.5 !!!.!..
112 ....!.!.!..!...!.... 20.5 !!!....
oben: 5 Folgen mit 5 Multiplikationen
19 !.!...!.!..!...!.... 20.6 !..!!
18 .!..!.!.!..!...!.... 20.6 !..!.
oben: 2 Folgen mit 6 Multiplikationen im niedrigsten Block
Die nächste Darstellung i=23 hat gegen oben eine andere Sortierung der Spalten !!
Bitte beachten Sie den symmetrischen Verlauf:
Dualzahlen links und Collatz-Folge rechts (Ausdruck von KK.exe)
! = 1 . = 0 ! = Multiplikation . = Division
n = 2^23 Permutation der ungekürzten
i m Dualzahl zu n Collatz-Folge zu Zahl n
23.00 !....................... ....................... 8388608 Diff.:
23.01 !.!.!.!.!.!.!.!.!.!.! !...................... 1398101 0
23.01 !.!.!.!.!.!.!.!.!.!.. ..!.................... 1398100 1
23.01 !.!.!.!.!.!.!.!.!.... ....!.................. 1398096 4
23.01 !.!.!.!.!.!.!.!...... ......!................ 1398080 16
23.01 !.!.!.!.!.!.!........ ........!.............. 1398016 64
23.01 !.!.!.!.!.!.......... ..........!............ 1397760 256
23.01 !.!.!.!.!............ ............!.......... 1396736 1024
23.01 !.!.!.!.............. ..............!........ 1392640 4096
23.01 !.!.!................ ................!...... 1376256 16384
23.01 !.!.................. ..................!.... 1310720 65536
oberer Block jede Zeile 1 Multiplikation nach Collatz
unterer Block jede Zeile 2 Multiplikationen :
23.02 !!!...!!!...!!.!.! !.....!................ 233013
23.02 !!!...!!!...!!.!.. ..!...!................ 233012
23.02 !!!...!!!...!!.... ....!.!................ 233008
23.02 !!!...!!!...!.!.!. .!......!.............. 233002
23.02 !!!...!!!...!.!... ...!....!.............. 233000
23.02 !!!...!!!...!..... .....!..!.............. 232992
23.02 !!!...!!.!.!.!.!.! !...........!.......... 232789
23.02 !!!...!!.!.!.!.!.. ..!.........!.......... 232788
23.02 !!!...!!.!.!.!.... ....!.......!.......... 232784
23.02 !!!...!!.!.!...... ......!.....!.......... 232768
23.02 !!!...!!.!........ ........!...!.......... 232704
23.02 !!!...!!.......... ..........!.!.......... 232448
23.02 !!!...!.!.!.!.!.!. .!............!........ 232106
23.02 !!!...!.!.!.!.!... ...!..........!........ 232104
23.02 !!!...!.!.!.!..... .....!........!........ 232096
23.02 !!!...!.!.!....... .......!......!........ 232064
23.02 !!!...!.!......... .........!....!........ 231936
23.02 !!!...!........... ...........!..!........ 231424
23.02 !!.!.!.!.!.!.!.!.! !.................!.... 218453
23.02 !!.!.!.!.!.!.!.!.. ..!...............!.... 218452
23.02 !!.!.!.!.!.!.!.... ....!.............!.... 218448
23.02 !!.!.!.!.!.!...... ......!...........!.... 218432
23.02 !!.!.!.!.!........ ........!.........!.... 218368
23.02 !!.!.!.!.......... ..........!.......!.... 218112
23.02 !!.!.!............ ............!.....!.... 217088
23.02 !!.!.............. ..............!...!.... 212992
23.02 !!................ ................!.!.... 196608
usw. bis zur kleinsten Folge mit 7 Multiplikationen:
23.07 !!..! !..!.!...!.!..!...!.... n = 25
Lieber Leser, wenn Sie bis hierher gekommen sind, dann gibt es trotzdem kein Verdienstkreuz.
Aber es gibt die versteckte Freude an der Symmetrie von Dualzahlen und Collatz-Folgen. Und:
Der Hintergrund für den Beweis der Collatz-EINS sollte klar geworden sein !!
Primzahlen oder die Magie der Zahlen http://euroware.de von Reinhold Kiebart
Auch das hier behandelte Thema finden Sie dort in einer brillanten Präsentation, mit
einem superschnellem Suchprogramm in einer Windowsprogrammierung unter KK.exe.
Erstes
Datum dieses
Textes: 29. April 2009
Willi Jeschke
Copyright
© 2009
