Die komprimierte Collatz-Folge     ( oder: Coll-Punkte )

   
Bei den Untersuchungen zu Neues bei Collatz-Folgen entstand nebenbei ein neuer Algorithmus, der die klassische Collatz-Vorschrift exakt ersetzt. Die Sache ist interessant und führt zu obigem Titel.

Wiederun ist die besondere Folge von n=27 ein optimales Demonstrationsobjekt.
Die erste Abbildung zeigt die 'gekürzte' Collatz-Folge, mit verschiedenfarbig angelegten Zahlen.
Gerade Zahlen:  türkis (grün)              Ungerade Zahlen:  weiß ... bzw. magenta (lila)
( Die beiden längsten Balken 3644 und 4616 sind nicht maßstabsgerecht. )
 
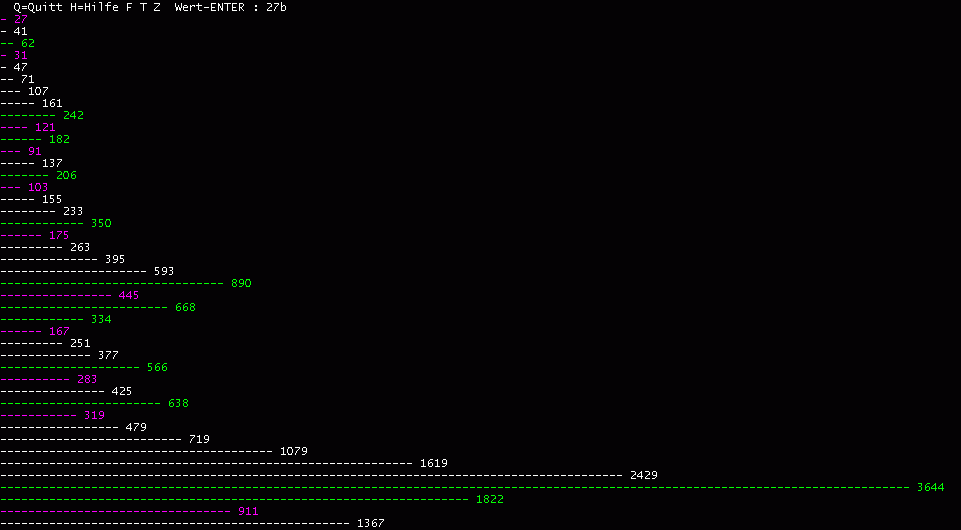
collatz grafik a
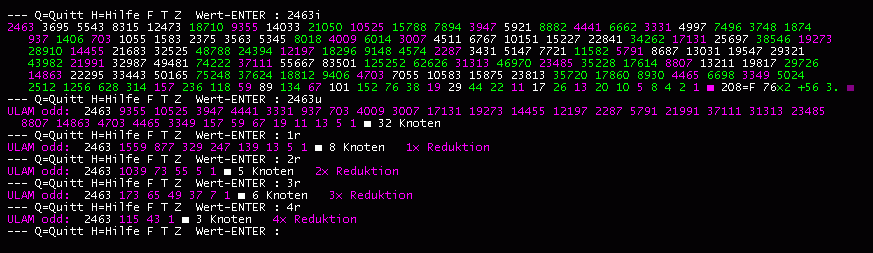
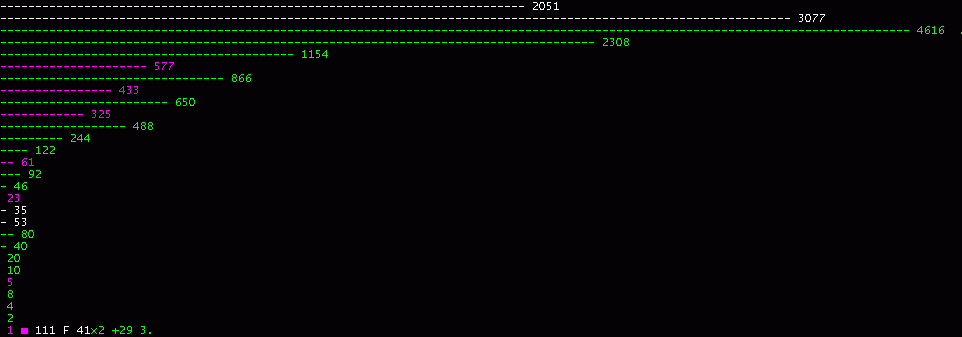
 collatz grafik b

In dem Bild sind bestimmte ungerade Collatz-Zahlen 'magenta' markiert. Man erkennt sofort, daß es sich jeweils um die erste oder eine einzelne ungerade Folgenzahl handelt. Genau diese Werte werden über die neue Rekursionsvorschrift ermittelt. Man kann das Resultat als 'komprimierte Collatz-Folge' bezeichnen. Diese Zahlen sind das Gerüst der Collatz-Folge. Alle anderen Zahlen könnte man weglassen, sie irritieren uns - schon seit Jahrzehnten. Ich halte es für angebracht, diesen besonderen Collatz-Zahlen einen eigenen Namen zu geben, zumindest zur besseren Verständigung. Mein Vorschlag:  'Coll-Punkte'  !!

 
   Ableitung der Rekursion für die ungeraden Coll-Punkte:

■ Jede gerade Zahl kann auf eine ungerade Zahl zurückgeführt werden (2er Division).  
■ Jede ungerade Zahl läßt sich schreiben            n = k * 2^j -1    
   Die nächstgrößere gerade Zahl ist dann      n+1 = k * 2^j
   k ist ungerade und >=1           (Mit k=1 und j>1 ist n eine Mersenne-Zahl.)  

■ Die Rekursion für die Coll-Punkte findet man aus        n  = k*2^j -1      
   und aus der Collatz-Vorschrift für die gekürzte Folge     n' = n*3/2 +1/2
   n' = (k * 2^j -1) * 3/2 +1/2  = (k *2^j *3 -3 +1) / 2 =  k *2^(j-1) *3^1 -1
   Für j=1 ist  2^(j-1)=2^0=1  und statt  3^1 wird für  j=1 ... 3^j    
   Führt man die Entwicklung weiter für j>1 bestätigt sich diese Beziehung !!
   Man erhält den geraden Wert       n' = k*3^j -1 ,   ... aus  n=k*2^j -1 
   und mit 2^e als Teiler von n'        n' = k' * 2^e      
   damit ist der ungerade, reduzierte Wert     n' = (k *3^j-1) / 2^e
                                                                
■  Die Rekursion ( je-Algorithmus, nach den Potenzen j und e)
    kann in einer speziellen Kettenbruch-Entwicklung geschrieben werden:
 
              (n+1)
             --------  * 3^j   -1                
                2^j    
    n' = -----------------------                        
                        2^e                       oder ...

    n' = ( ( (n+1) / 2^j ) * 3^j -1) / 2^e    wobei gilt..

    2^j   ist die größte in n+1 aufgehende Zweierpotenz    und            
    2^e  ist die größte in ( (n+1) / 2^j ) * 3^j  -1 aufgehende Zweierpotenz   
... das Ganze nochmals in einfachem Basic-Code,
     der prinzipiell auch die schrittweisen Collatz-Werte liefert:

  ' Für jeden ganzzahligen, positiven Startwert n>1 gilt:
  PRINT n
  DO UNTIL n=1
    n=n+1   :       j=0
    WHILE n MOD 2=0
      n=n/2 :       j=j+1
    WEND
      n=n*3^j -1 :  e=0
    WHILE n MOD 2=0
      n=n/2 :       e=e+1
    WEND
    PRINT n
  LOOP
  ' Ergebnis mit n=27 :
  ' 27 31 121 91 103 175 445 167 283 319 911 577 433 325 61 23 5 1     


Die endgültige Rekursionsformel für Coll-Punkte lautet somit...        

n' = (((n+1) / 2^j ) * 3^j -1) / 2^e             
 
■ ■ Bestimmend für den nächsten Coll-Punkt n' (... in der  Collatz-Folge) ist damit
      die 2er Potenz und das Produkt aller ungeraden Primfaktoren von  n+1

■ ■ Die Zahl n+1 hat - wie jede Zahl - eine eindeutige Zerlegung in Primfaktoren.
      Daraus folgt: Es gibt nur eine eindeutige Collatz-Folge zu der Zahl n.
 
Die Folge der Coll-Punkte im oberen Bild ist dann:        / Startzahl + 17 Coll-Punkte /
 
27  31  121  91  103  175  445  167  283  319  911  577  433  325  61  23  5  1
 
Für n = 103 ...  n+1 = 104 = 13*2^3 ... j=3    n'=(13*3^j -1)/ 2^1 = (351-1)/2 = 175

Von besonderer Bedeutung ist die Anwendung der Rekursion auch auf gerade Zahlen.
Nach Collatz werden diese sofort durch 2 auf eine ungerade Zahl reduziert (gekürzt).
Das gleiche Resultat muß auch die Rekursionsformel ergeben:
Ist  n  gerade, dann ergibt n+1 für 2^j=1, da  j=0 .   Somit ist auch 3^j=1  und
n' = (n +1 -1) / 2^e = n / 2^e   ... das entspricht exakt Collatz,
für  n=104  ist  k=105*2^0=105  und  n'=(105-1)/2^3=104/8=13 .
 
Was zeichnet die 'Coll-Punkte' aus,  gegenüber den Collatz-Einzelschritten?
  
Der bekannte Collatz-Algorithmus ist ein iteratives Verfahren, es ist ein 'Probieren'. Bisher konnte man kaum erkennen, von welchen Zahlen das Ergebnis konkret beeinflußt wird. Man notierte zwangsläufig mehrfach hintereinander ungerade und gerade Werte, die nach gegebener Vorschrift gefunden wurden. Ein logischer Aufbau, eine Struktur war nicht erkennbar...  'hailstone numbers'.
Die rekursiv berechenbaren Coll-Punkte liefern diese Struktur. 
Selbstverständlich sind die beiden Folgen 'Collatz-Einzelschritte' und 'Coll-Punkte' vollkommen kompatibel. Jede Zahl einer Folge erlaubt den Übergang zu der anderen Darstellung. Dahinter verbirgt sich kein Trick, nur etwas einfache Algebra. Sie führt zu einer Art 'Kettenbruch'.
 ( Bei einem regulären Kettenbruch - alle Zähler gleich Eins - wird meist der Euklidsche Algorithmus verwendet. Dann gilt der Satz: Kettenbrüche rationaler Zahlen sind endlich. Das ist jedoch nicht zwingend bzw. übertragbar. Ich vermute, daß man für den hier verwendeten Algorithmus den Nachweis führen könnte, daß dieser spezielle Kettenbruch ebenfalls 'endlich' bei EINS endet.) 
 
Zusatzbetrachtung:
Als Näherung - besser als Krücke - könnte man die 3er und 2er Potenzen der Brüche
einfach zwischen die obige Collpunkt-Folge von n=27 schreiben, aber bitte mit Vorsicht :
(27+1).9/8.(31+..).243/64.121.3/4.91.9/8.103.27/16.175.81/32.445.3/8.167.27/16.283...
...9/8.319.729/256.911.81/128.577.3/4.433.3/4.325.3/16.61.3/8.23.27/128.5.3/16.1
Das reziproke Produkt der Brüche ist  2^70 / 3^41 ist interessant. Denn: Die normalee Folge von n=27 hat 70 Divisionen und 41 Multiplikationen. Den Bruch  2^70 / 3^41 (= ~32) darf man jedoch nicht algebraisch auswerten. Es ist nur eine sehr grobe Näherung zu der Zahl 27, da die ±1_Werte der korrekten Rekursion hier unberücksichtigt sind.

Link zu 'Collatz-Folgen', damit auch zu den 'Coll-Punkten' (Berechnung + versch. Grafik):  
Primzahlen oder die Magie der Zahlen          http://euroware.de     von  Reinhold Kiebart

Der folgende blaue Text ist ein Thema am Rande:
 
    Kann man eine Collpunkt-Folge so beeinflußen, daß sie schneller zu  1  führt?
 
Die Coll-Punkte gestatten einen gezielten Eingriff durch eine 2er Reduktion, sehr ähnlich, wie es in der Collatz-Vorschrift allgemein für gerade Zahlen vorgegeben ist. Selbstverständlich ändert sich die Folge, sie läuft über 'andere' Zahlen... eben mit der Vorgabe, der schnelleren 1. In der Regel ist dies der Fall. Zwingend ist es nicht, es bleibt abhängig von den auftretenden Primfaktoren der 'anderen' Zahlen.  
Es war zu prüfen, ob innerhalb des gesamten Prozedere ein Ort existiert, an dem der Folgenverlauf zur 1 entscheidend behindert, begünstigt oder sogar erzwungen wird. Diesen Ort gibt es! Es ist die gerade Zahl der Rekursion  n+1 . Genauer gesagt: Die Potenz j des Primfaktors 2, die mit 3^j weitergeführt wird. Bedingung:  j > 0 .
 
Lösung durch Reduktion:
Dazu werden die 2er Potenzen der Zahl n+1 nur teilweise in 3er Potenzen umgesetzt.
Nehmen wir den Coll-Punkt 911 :
n=911  mit  n+1=912=2^4*57...   j=4   wird normal zu... 3^4*57=4617... (4617-1)/8=577   
Wir reduzieren den Wert j. In der Regel wird der nächste Coll kleiner sein, z.B.:
n=911  statt j=4 wird... j'=3 ... 3^3*57=1539... (1539-1)/2^3=769  
769 ist korrekt ermittelt und sogar größer als der normale Coll 577... gehört aber zu der nun veränderten Coll-Folge, die insgesamt schneller zu 1 konvergiert.  
Noch effektiver ist: n =911  statt j=4 wird... j'=2 ... 3^2*57=513...  (513-1)/2^9= 1  

Die folgende Tabelle zeigt die Möglichkeiten der teilweisen Reduktion von Zahl  912.
Nur j=2  liefert das direkte Ende mit dem gesuchten Ziel n=1. Dieser Sonderfall
tritt nur dann auf, wenn mit  k*3^j -1 eine reine 2er Potenz getroffen wird, hier  512.

 j  57*2^j  3^j  (57*3^j -1)  Coll
                              neu      
 4    912    81     4616      577  'soll' nach Collatz
 3    456    27     1538      769  'ist' für j=3 statt j=4
 2    228     9      512        1   und j=2 liefert sofort die 1
 1    114     3      170       85             
(0     57     1       56        7)

Nächstes Bild:
Oben...   normale, verkürzte Collatz-Folge für n=27
Mitte...   Coll-Folge 
Unten...  Coll-Folge für n=27 (zu Collatz) ...  bis Coll 911, dann sofort 
              mit gezielter Reduktion über 2^2 auf  1   (obiges Beispiel)  
 
Ulam Resultat

Noch deutlicher kann man die Reduktion zeigen, wenn man sie nicht nur bei einer Zahl in der Folge ansetzt, sondern wenn bei jedem Schritt der Exponent j verkleinert wird, z. B.  für  die Zahl 2463.
Im Bild bedeutet:  '2x Reduktion'...  Die 2er Potenz der Zahl  n+1=2464=2^5 * 77 wurde auf 2^3 reduziert. Die maximale Reduzierung kann bis auf 2^1 gehen, 2^1 ist das Minimum. Statt der Folge mit 32 Colls erhalten wir kürzere Folgen, hier  8,5,6 und 3 Coll-Punkte (Knoten).
Man kann sich auch darauf einigen:    Immer Reduktion auf 3, statt 3^j!
Das ergibt teilweise neue oder vollkommen neue Coll-Punkte bis herunter zu EINS.
 
Ulam Reduktion total

Es stellt sich jedoch die Frage:  
Will man wirklich das schnelle Ende der Folgen?  Der Spaß am Collatz Zick-Zack wäre verloren !
Wir wollten doch nur wissen, ob und wie es geht. Das Wissen wird uns genügen !
Trotzdem wurde dazu eine neue Übersicht erstellt: Die 4 Collatz-Folgen