Primzahlen und Collatz- Ulam- 3n+1 Zahlenfolge

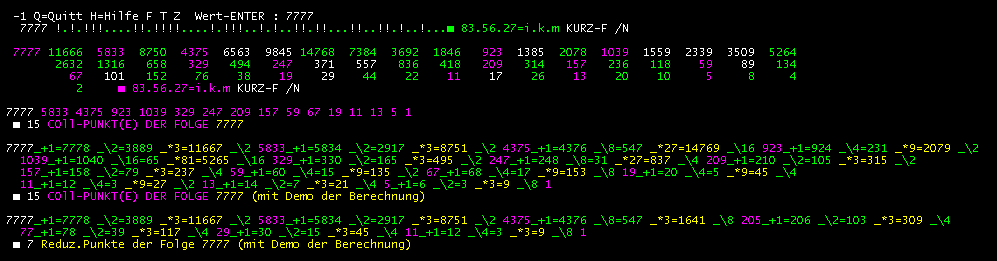
Die 4 verschiedenen Collatz-Folgen

In der Literatur kennt man nur zwei verschieden lange Collatz-Folgen:

1. Normale Collatz-Folge mit dem (Multiplikations-) Schritt 3n+1
2. Gekürzte Collatz-Folge mit dem kombinierten Schritt (3n+1)/2
Hier wird die erste Division nach einer Multiplikation nicht ausgegeben.

Unter Die komprimierte Collatz-Folge wird gezeigt, daß über eine Rekursionsformel ausgesuchte Collatz-Punkte definiert werden können. Diese sind immer ungerade und werden als sogenannte Coll-Punkte bezeichnet. Die Folge wird benannt:

3. Komprimierte Collatz-Folge Rekursion... n' = (((n+1) / 2^j ) * 3^j -1) / 2^e
Diese Folge ist absolut kompatibel mit den bisher bekannten 3n+1 Folgen 1. und 2.

Nun läßt sich eine weitere Reduktion der bereits komprimierten Folge einführen.
Am einfachsten: Das Multiplikationsglied 3^j wird durch 3^1 , also durch 3 ersetzt:

4. Reduzierte Collatz-Folge Rekursion... n' = (((n+1) / 2^j ) * 3 -1) / 2^e
Diese neue, meist kürzere Folge ergibt teilweise neue oder auch
vollkommen neue Glieder... selbstverständlich wieder herunter bis zu 1.

Alle vier Folgen basieren letztlich auf dem gleichen Prinzip !
Die Primfaktoren von n+1 sind der zentrale, bisher nicht erkannte Schlüssel !

Das nächste Bild zeigt 5 verschiedene Darstellungen der Folge n=7777.
Als Demo zu beachten sind die gelb angezeigten Multiplikationen in der unteren Bildhälfte:
Einmal sind es versch. Potenzen von 3, dann durchweg nur der Faktor 3.
Die erzeugten Coll-Punkte bzw. Folgenwerte haben die Farbe magenta (lila).

Collatz Folgen