Primzahlabstände, Primzahlzwillinge, Funktion Relative Häufigkeit

Primzahlzwillinge: 'Einheit' aller Primzahlabstände

Worum geht es hier? Einfache Zusammenhänge sollen aufgezeigt werden, zu dem Thema:
Abstände zwischen beliebigen, ungeraden Primzahlen.
Daß es sich dabei immer um gerade Zahlen a=2*k handelt, ist trivial. Die Anzahl einzelner Abstände in einem beliebigen Intervall wird mit pi.2k bezeichnet ( k>0 ). Für die Anzahl von Primzahlzwillingen mit Abstand a=2 setzt man pi.2... ( k=1) /... man liest auch pi.a(x) x=Schranke /
Nun sucht man seit Jahrhunderten vergeblich einen Beweis unendlich vieler Primzahlzwillinge.
Selbst wenn heute Arbeiten dazu vorliegen, so bleiben diese - ohne ein Studium der Mathematik - nur schwer verständlich.

Sieht man das Problem dagegen breiter - nicht nur eng auf Zwillinge ausgerichtet - dann wird man überrascht feststellen:

pi.2 ~ pi.2^n ~ pi.2p ..... Was bedeutet das in einer ersten Abschätzung?

Jeder Primzahlabstand, der das Doppelte einer hinreichend großen Primzahl ist, wird - als grober Richtwert - etwa so häufig auftreten, als in dem Bereich Primzahlzwillinge vorhanden sind! Ich nannte diese Anzahl an anderer Stelle 'Grundmenge M0'.

Auch Primzahlabstände, die reine 2er Potenzen sind, werden etwa in dieser Anzahl vorkommen.

Und andere Abstände? Ihre Anzahl ist in der Regel größer als M0 und sie ist abhängig von den Primfaktoren des Abstandes!

Es gilt: Je größer die Anzahl verschiedener (ungerader) Primfaktoren ist, desto häufiger wird ein solcher Abstand anzutreffen sein.

Zusammengefaßt: Jeder beliebige Primzahlabstand tritt gleich oft oder öfter auf, als Primzahlzwillinge vorhanden sind.
Die gegebene Grundmenge M0 - Anzahl der Primzahlzwillinge - wird nicht unterschritten.
Immer vorausgesetzt, daß die betrachtete Zahlenmenge die notwendige Größe besitzt.

Gibt es gerade Abstände die prinzipiell nicht auftreten? Nein! Jede natürliche, gerade Zahl ist als Primzahlabstand in einem hinreichend großen Intervall vorhanden. So schwierig der klassische Beweis dafür ist, so einfach ist die Berechnung/Abschätzung der gegebenen Daten:

Analog zur Zahl 1, die als Einheit der Zahlen definiert wurde, muß man die
Primzahlzwillinge (mit obigem k=1) als die 'Einheit aller Primzahlabstände' sehen. Es gilt:

In jedem beliebig hoch gelegenen, hinreichend großen Zahlenintervall sind alle geraden Primzahlabstände - auch Primzahlzwillinge - in einer abschätzbaren Mindestanzahl M0 vorhanden.

10^s Stellenzahl einer beliebig hohen Schranke x x = 10^(10^s)
für circa M0=250 Primzahlzwillinge (theoretisch 249) gilt die einfache Beziehung:
Stellenzahl des Intervalls si = 2*s +3 ... somit Intervall Iv = 10^(2*s +3)

Diese Grundmenge M0 der Primzahlzwillinge ist ein wichtiger Wert. Man erhält ihn über 1/ln^2 und aus heuristischen Überlegungen über die sogenannte Primzahlzwillingskonstante C=1.32032...
Ableitung der einfachen Formel: Analogie zu Euklid - Primzahlzwillinge

Ein enger Beweis für einen einzelnen fernen Primzahlzwilling muß nicht geführt werden. Wichtiger ist, zu erkennen, daß bei einer hinreichend großen Anzahl laufender Primzahlen jeder beliebige, gerade Zahlenwert >=2 als Abstand zwischen Primzahlen tatsächlich vorhanden und seine Menge in guter Näherung abhängig von jener Grundmenge M0 direkt zu berechnen ist. Das gilt ohne Einschränkung für jedes entsprechend große Zahlenintervall an jeder beliebigen Stelle (Schranke), auch im 'abzählbar' Unendlichen !!!

Mehr zu dem Thema... Konzentrat: "Relative Häufigkeit von Primzahlabständen"

Deutlich unterstreiche ich hier für jeden Leser:
Die folgenden Bilder dienen absolut keinem Beweis. Sie sind nur eine Erläuterung gegebener Tatsachen, um den Zusammenhang zwischen den Primfaktoren eines Primzahlabstandes und seiner Häufigkeit in einem beliebigen, großen Intervall aufzuzeigen - oder als negatives Gegenstück - in einem zu kleinen Bereich (!).

Als 'großes' Intervall wurde hier 1 Million Zahlen gewählt, oberhalb einer Schranke von 100 Millionen.
Jedes andere große Intervall liefert vergleichbare Werte mit: pi.2 ~ pi.2p

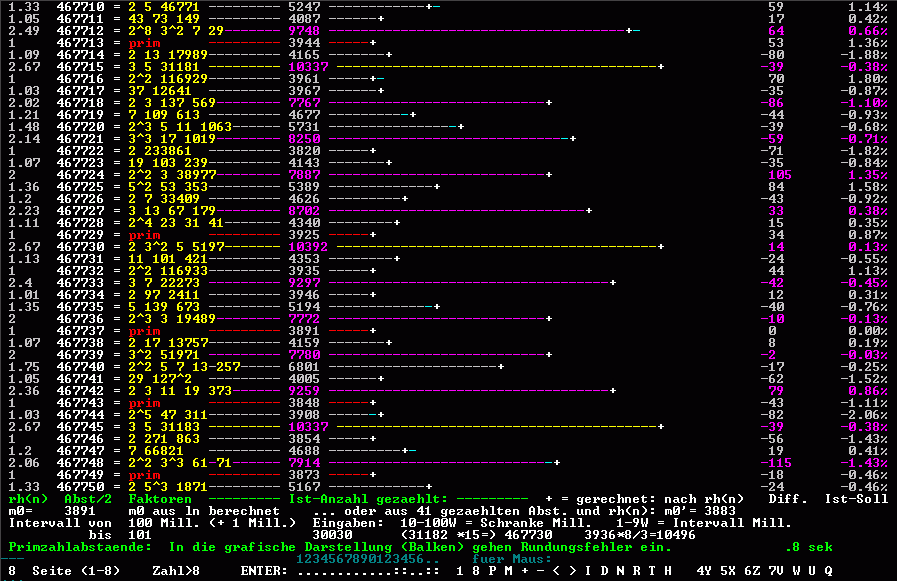
primin18w hohe Werte

Inhalt der einzelnen Spalten von links nach rechts:
( Das untere Bild zeigt eine Animation mit primini.exe )

rh(n)    Faktor der Funktion 'relative Häufigkeit' gegenüber M0 = pi.2 hier... M0=3891
Wert halber Primzahlabstand (weiß)
Wert    Primfaktoren des halben Primzahlabstandes (gelb)
Wert    pi.2k gezählte Menge der Primzahlabstände im Intervall, dazu eine Balkengrafik:
Balken darunterliegend -----------* mit + = berechneter Wert nach rh(n) (weiß = Soll)
ganz rechts Zahl der Primfaktoren und Werte zu Differenz = Ist - Soll    (magenta=Ist)
Farben: rot    Primzahl
magenta durch 3 teilbar
  gelb durch 3 und 5 teilbar
grün letzter gezählte Wert, liegt eventuell unter dem +

Beachten Sie z. B. die 3 gelben Balken im oberen Bild: Diese Abstände haben die kleinen Primfaktoren 3 und 5 gemeinsam... und wie häufig sind diese Abstände? Daß der Zahlenwert 10337 exakt zweimal auftaucht, ist eine echte Ausnahme, die ich erst beim Tippen dieser Zeilen feststellte. Das ist nicht ausgesucht!
Oder prüfen Sie bitte die Anzahl der 5 Abstände, deren k=a/2 prim ist... wie auch k/2=467732=4*116933 .... und andere.

Ergänzung: Kleinere Intervalle
Was zeigen diese? Von links nach rechts, Intervalle mit 10.000, 1.000 und 100 Zahlen:
Beachten Sie im rechten Bild: Zuerst tauchen in der Regel jene Abstände auf, die bei größeren Intervallen (mittl. Bild und links) am häufigsten sind. Deshalb ist es notwendig , daß ein betrachtetes Intervall immer eine 'hinreichende' Größe besitzt.
Siehe dazu auch:   Analogie zu Euklid - Primzahlen - Primzahlzwillinge

Link: Ein interessantes Pimzahlprogramm von Reinhold Kiebart, das neben vielen anderen Möglichkeiten auch Primzahlabstände berechnet und darstellt, finden Sie als Download (kostenlos) unter:
Primzahlen oder die Magie der Zahlen

Schlußpunkt
Wenn nun die Mengen aller Primzahlabstände untereinander so interessant verflochten sind, dann müßte eine Reduktion [über rh(n)] auf jene Grundmenge M0 flächendeckend für Intervalle und Abstände gut dargestellt werden können. Hier ein Versuch dazu:
In den folgenden Tabellen sollten alle weißen Werte der Grundmenge M0 den Wert 1000 anzeigen. Denn jedes Intervall (Zeile 1-12) ist so gewählt, daß etwa 1000 Zwillinge zu erwarten sind. Und aus jedem gewählten und gezählten Abstand (Spalte 4-13) wird über die Funktion rh(n) eine Grundmenge M0' berechnet, die dann ebenfalls bei 1000 liegen muß. Mit einem Blick kann man die 'Streuung' der reduzierten Mengen der tatsächlichen Primzahlabstände und der Zwillinge genüber dem zu erwartenden Sollwert 1000 erkennen.
Nebenbei: Rechts ist ( rot ) für Intervalle und Primzahlabstände die Standardabweichung der Mengen bezogen auf den Mittelwert angegeben, auch grafisch. - Zu beachten ist die Größe der Intervalle, sie ist quadratisch abhängig von der Schranke 10^x !!

Reduzierte Primzahlabstände: pi.a' = pi.a / rh(n) ... soll = 1.000
Beim mittleren Bild (2er Potenzen) ist keine Reduktion erforderlich.

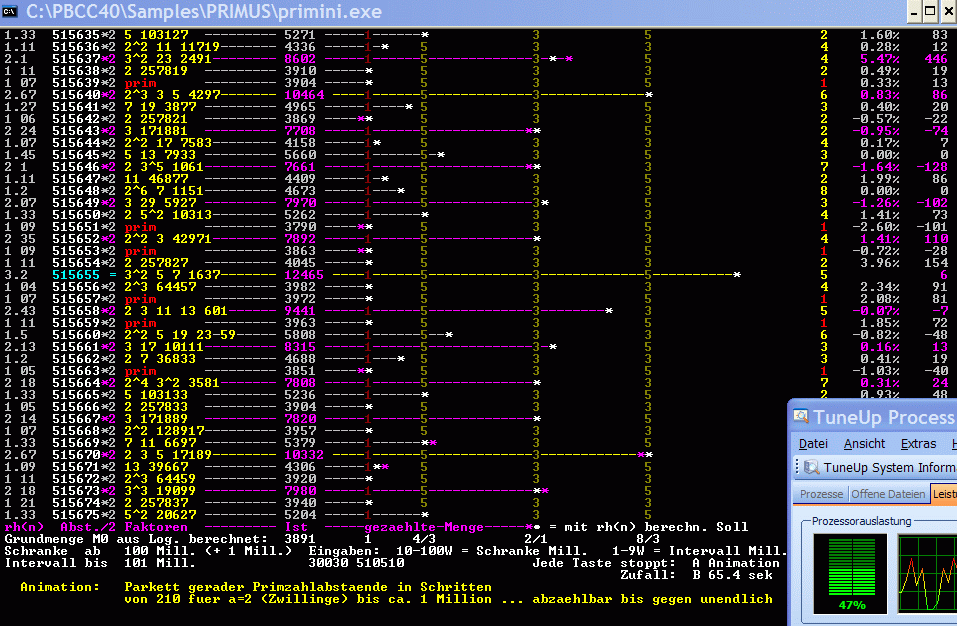
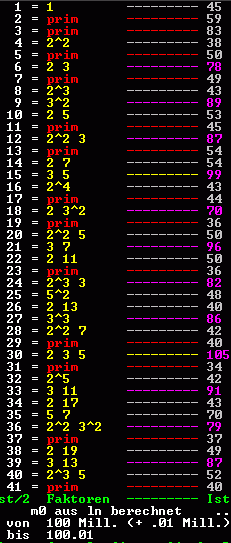
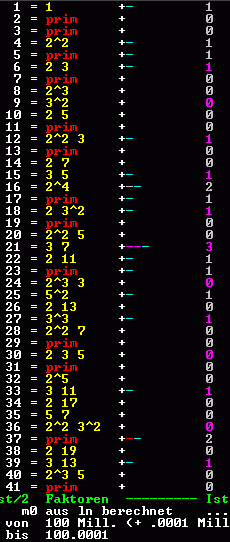
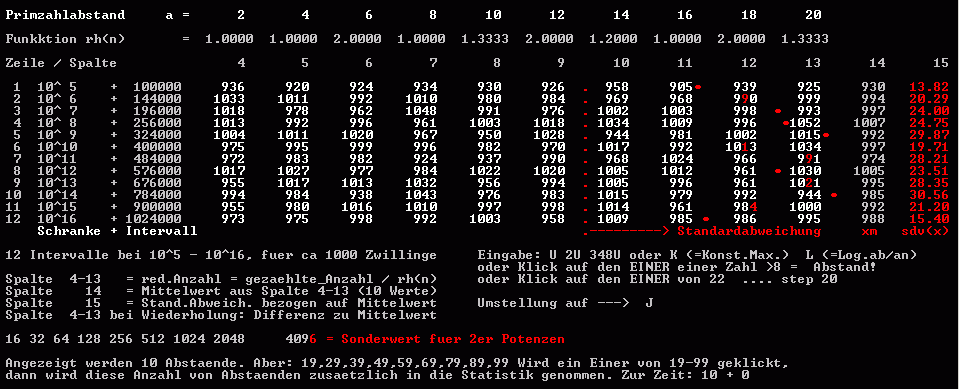
Abstände 2-20

Resultat der Untersuchungen auf dieser Seite:
Will man Primzahlabstände bearbeiten und aussagekräftige Ergebnisse erhalten, dann sollte das gewählte Intervall eine bestimmte Grundmenge M0 von Abständen enthalten. Größere Abstände sind in der Regel häufiger oder gleich häufig. Aus der Erkenntnis dieser Zusammenhänge leitet sich die Existenz des Einzelabstandes a=2 - also Primzahlzwillinge - zwingend ab.

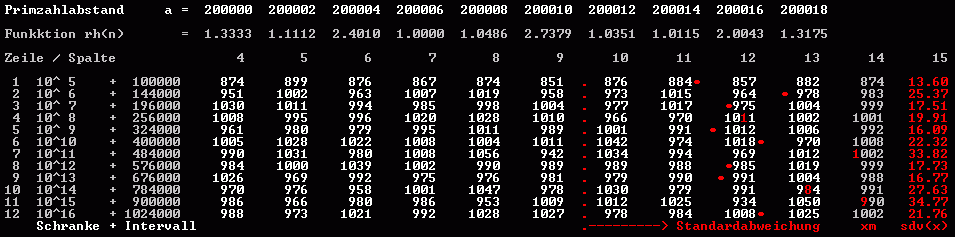
Zweckmäßige Grundmenge m0 für Primzahlzwillinge und gleichwertige Primzahlabstände:
100, 250 bis 1000 Zwillinge (Primzahlabstände) pro Intervall

Das Ganze dürfte für Sie neu gewesen sein. Wenn es Spaß machte, freut es mich. Denn nicht jeder hat ein entsprechendes Programm zur Verfügung. Diese Seite sollte nur zusätzliche Informationen vermitteln und nichts beweisen. Daß ich ähnliche Untersuchungen auch mit weit höheren Stellenzahlen durchführte, muß ich nicht betonen. Die Anzeige dieser Inhalte würde das vorhandene Format sprengen. Vor allem aber, könnte daraus der falsche Schluß gezogen werden, daß meine Aussagen zu dem Thema über irgendwelche Statistiken gewonnen wurden. Das ist absolut unzutreffend.

Dennoch, ein nützlicher Nachtrag: Hoher Bereich: Experimentelles zu P.-Abständen