Die Gesetzmäßigkeit der Primzahlabstände im unendlichen Zahlenraum !
Unten, auf dieser Seite: Zusammenfassung
Meine Überlegungen von 2004 zu diesem Thema wurden bisher nur begrenzt aufgenommen, bezw. von Mathematikern mit Namen abgelehnt! Im Juni 2005 sah sich Herr Thomas Kantke aus München die Sache an. Er schrieb sehr überraschend:
• Ihre Ausarbeitung wird als Spezialfall von einer allgemeineren Behauptung erfasst, die 1923 von den Mathematikern Hardy und Littlewood aufgestellt worden ist. •
Nachlesen kann man es in dem Buch "The New Book of Prime Number Records" von Paulo Ribenboim (Springer Verlag, z.Zt. vergriffen ? ). Hier ist die Originalzeile, wobei k >= 1 und C2 die sogenannte Primzahlzwillingskonstante (= 0.66016...) ist:
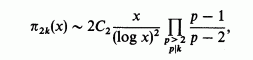
H+Li machen keine besonderen Angaben - soweit mir bekannt - zu der Konstanz der 'relativen Häufigkeit' von Primzahlabständen in beliebig gelegenen Intervallen innerhalb unseres Zahlensystems. Doch genau dort liegt mein beinahe trivialer Ansatz, dazu die folgende Darstellung von Intervallen:
o----|---------|------|--------|---------------|---------|-------Intervall-------->
o-----|-------|----------------|----------Intervall--------|-----------|---------->
Die Skizze zeigt zweimal die Zahlengerade unterteilt in völlig beliebige, große Intervalle.
Für jedes einzelne, hinreichend große Intervall gilt meine Aussage, nicht nur allgemein für Zahlen unterhalb einer Schranke x. Das schließt ein, daß auch jedes zunächst 'letzte Intervall' die gegebene relative Häufigkeit der Primzahlabstände aufweist - wobei durch den oder die Unendlichkeitsbeweis(e) von Primzahlen feststeht, daß es jenes 'letzte Intervall' nicht gibt.
Nach dieser Vorbemerkung kann ich meinen Text ohne jede Änderungen stehen lassen. Die Faszination, die von dem Thema ausgeht, wird durch den "alten Hut" der bekannten Mathematiker nur gestärkt. Meine Überlegungen - ausgehend von Intervallen - werden durch die von H+Li allgemein angegebene Vermutung zur Verteilung der Primzahlen geradezu herausgefordert.
Unabhängig vom
Ort eines Intervalls
gilt für jedes hinreichend große Intervall:
Die Mengen (Anzahl) aller Primzahlabstände
a>=2
stehen untereinander in einem vorgegebenen Verhältnis.
Die relative Häufigkeit jedes beliebigen Primzahlabstandes
ist direkt abhängig von seinen Primfaktoren.
- Korrekte Definition von Intervall und Primzahlabstand
- Zahlenabstände zwischen den 'möglichen' Primzahlplätzen
- Funktion der 'relativen Häufigkeit' rh(n)
- Zahlenabstände zwischen den 'tatsächlichen' Primzahlen
Wichtig: In dieser Darstellung und zur Entwicklung der Funktion rh(n) wurde keinerlei Statistik oder Zahlenmaterial verwendet.
1. Definition
von Intervall und
Primzahlabstand
Vorbemerkung: Als Primzahlabstand wird
sowohl der Abstand
zwischen aufeinaderfolgenden Primzahlen sowie
zwischen zwei
nicht aufeinanderfolgenden Primzahlen bezeichnet.
Zwingend
ist:
Ein Primzahlabstand a gilt dann als 'innerhalb eines
Intervall Iv liegend', wenn der Anfang des Abstandes innerhalb von
Iv liegt. Das Ende kann außerhalb liegen. Nur so sind
relative Häufigkeiten ohne Einschränkungen gegeben! (Sinngemäß kann man
auch die Enden
innerhalb von Iv liegend festlegen. Der Anfang kann dann
außerhalb liegen.) - Empfehlung, keine
Bedingung: Die betrachteten
Primzahlabstände sollten kleiner als das
Intervall sein.
2. Zahlenabstände zwischen 'möglichen'
Primzahlplätzen
Solche
Abstände entstehen, wenn man die Zahlengerade
mit einem modulo-Muster
'parkettiert', also fortlaufend belegt. Welcher Modul m verwendet wird,
ist zweitrangig.
Geht man davon aus, daß nur ungerade Zahlen >2
Primzahlen sein können, hat man bereits
mod 2 angewandt. Die nächsten Module wären 6 (=2*3)
oder 30 (=2*3*5). Natürlich auch jedes
weitere primoriale Produkt ansteigender Faktoren, etwa 2310 (=2*3*5*7*11).
Hier soll wegen
der besseren Übersicht
mod 30 verwendet werden. Die
Zahlengerade,
dargestellt in der ersten Zeile, sieht
dann an
jeder beliebigen Stelle so
aus:
--•|•-----•---•-•---•-•---•-----•|•-----•---•-•---•-•---•-----•|•-----•---•-•----- -1|1 7 11 13 17 19 23 29|1 7 11 13 17 19 23 29|1 Block mod 30 •-----•-----• •-------------------• a=6 a=6 a=20 |
Es ist hinlänglich bekannt und bewiesen: Jede Zahl, die mod 30 einen der Reste 1, 7, 11, 13, 17, 19, 23 oder 29 liefert, ist möglicherweise eine Primzahl. Oder anders betrachtet: Verwendet man das viel besprochene 'Sieb des Eratosthenes', dann ist obige erste Zeile eine Abbildung der Zahlengeraden nach den Streichungen durch die Primfaktoren 2, 3 und 5. Dabei ist jedes 'minus' eine nach Eratosthenes gestrichene Zahl und jedes Zeichen • ein verbleibender 'möglicher' Primzahlplatz.
In der 3. Zeile sind
drei beliebige Abstände eingetragen...
zweimal a=6 und
einmal a=20.
Bereits durch einfaches Abzählen kann ermittelt
werden, wie
oft ein
'möglicher' Primzahlabstand in einem 30-er Zahlenblock
auftritt. Wohlgemerkt: ein 'möglicher', kein
'tatsächlicher'.
Das Zählen beginnt immer
in einem ersten 30-er Block und endet spätestens im zweiten
Block.
Für größere modulo-Werte ist die Verwendung eines Zählprogramms sinnvoll.
Als
Resultat des Zählens wird man die
Häufigkeit der Abstände pro 30-er Block feststellen
mit:
pi.a .... Anzahl der
Abstände a
pi.2
.... Anzahl Zwillinge
a=2
(pi.2
= Grundmenge M0)
Abstände, nur mit Primfaktor
2 a=2,4,8,16,32 pi.a = pi.2
= 3
Abstände, ein ungerader Faktor 3
a=6,12,18,24 pi.a = pi.2
* 2/1 = 6
Abstände, ein ungerader Faktor 5 a=10,20
pi.a
= pi.2 * 4/3 = 4
An dem Abstand 30 mit den Faktoren 3 und 5 läßt sich
besonders einfach erkennen:
pi.30
= pi.2 * 2/1 * 4/3 = 3*2*4/3
= 8
Ohne jede Formel findet man dazu die einfache Bestätigung,
denn...
Alle 8 Primzahlplätze eines 30er
Zahlenblocks haben mod 30 ihren Partner!
Andere
Abstände (14, 22, 26, 28...) auszuwerten
macht wenig Sinn , da diese die noch
nicht gestrichenen Primfaktoren 7, 11, 13... enthalten. Dazu
müßten höhere modulo-Werte
für die Parkettierung eingesetzt werden. Diesen Schritt kann
man sich jedoch sparen, denn die Funktion der
'relativen Häufigkeit' rh(n) liefert die korrekten Werte für
alle
Primfaktoren in allgemeiner
Gültigkeit,
ohne jede Begrenzung bis 'abzählbar unendlich'
!
3. Funktion
der 'relativen Häufigkeit'
Diese gibt an, wie
häufig ein Primzahlabstand in einem
Intervall auftritt - in Abhängigkeit von den
Primfaktoren
des Abstandes. Haben die Primfaktoren eventuelle
Potenzen h_, dann gilt mit f0=2 und h0>0 (Potenz von
2) :
Abstand a_n = f0^h0 * f1^h1 * f2^h2 * f3^h3 * ... fk^hk
Die
Anzahl eines
Primzahlabstandes ist abhängig von der Grundmenge M0
(PZ-Zwillinge)
und den ungeraden Primfaktoren f1
bis fk des Primzahlabstandes:
rh(n) ~ M0 * (f1-1)/(f1-2) * (f2-1)/(f2-2) *..... (fk-1)/(fk-2)
Die Grundmenge M0 ( = Menge
der
Primzahlzwillinge = pi.a2 )
kann auch mit M0=1 angenommen werden.
Somit gilt z.B. für den Primzahlabstand 25.410=(2)*3*5*7*11^2
die Funktion der relativen Häufigkeit rh(n) mit M0=1
rh(n) ~
1 *2/1 *4/3 *6/5 *10/9
= 32/9
(2)
(3) (5) (7) (11)
Der Primzahlabstand 25.410 und
alle
anderen
Abstände, die die gleichen Primfaktoren mit beliebigen
Potenzen
>0 enthalten, werden somit in jedem größeren
Intervall etwa 32/9 mal so oft auftreten,
als Primzahlzwillinge in
diesem Intervall enthalten sind.
4. Zahlenabstände
zwischen 'tatsächlichen'
Primzahlplätzen
... hierzu auch: Grafik
zu Primzahlabständen
Die relative
Häufigkeit
der 'tatsächlichen' Primzahlabstände geht hervor aus
der
relativen Häufigkeit der Zahlenabstände
zwischen den
'möglichen'
Primzahlplätzen. Wie ist das erklärbar?
Die eigentliche Ursache liegt in der nur 'scheinbar
zufälligen'
Primzahlverteilung!
Tatsächlich ist in der
strengen Gesetzmäßigkeit
der natürlichen Zahlenfolge enthalten, daß beim
Streichen
von
Primzahlplätzen
(...nach Eratosthenes) auch Primzahlabstände mit der gleichen Gesetzmäßigkeit gestrichen werden. Resultat: Die
relative Häufigkeit der
Funktion rh(n) vor dem Streichen gilt mit sehr guter
Näherung
auch für die relative Häufigkeit nach dem
Streichen - bis abzählbar unendlich!
Voraussetzung hierfür ist, daß
das Intervall hinreichend groß
gewählt wird.
Eine konkrete Zahlenangabe* hierzu ist nicht
erforderlich, es existiert
auch keine Obergrenze. Es stehen unendlich viele
Primzahlen
zur Verfügung, wodurch die Forderung nach einem geeigneten
Intervall immer erfüllt werden kann. Die
berechenbare Relation zwischen den einzelnen
Primzahlabständen - also zwischen der Anzahl
eines beliebigen
Primzahlabstandes und der Anzahl von Zwillingen -
ist immer gegeben.
*
Eine einfache
Abschätzung kann
jedoch für jede 10er Potenz (Schranke) gemacht
werden.
...siehe auch: Analogie
zu
Euklid - Primzahlen - Primzahlzwillinge
Man wird meinen Text als 'Prosa' bezeichnen, die den Axiomen der Mathematik nicht genügt. Einverstanden! Aber diese Prosa ist 'wahr'. Die existierende Gesetzmäßigkeit der Primzahlabstände wurde bisher eher übersehen als erkannt. Sie muß und wird in irgend einer Weise Eingang finden in die Theorie der Zahlen, auch im Hinblick darauf, daß die heutigen Möglichkeiten der experimentellen Mathematik andere sind als vor 100 Jahren.
Daß ich nachträglich ausgedehnte numerische Kontrollen vorgenommen habe, auch in hohen Bereichen bei 1000 und 100.000 Dezimalstellen, ist selbstverständlich. Die erwartete Übereinstimmung ist mehr als zufriedenstellend.
| Zusammenfassung:
Die
Funktion der relativen Häufigkeit rh(n) gilt
unabhängig vom Ort eines
Intervalls. In Anbetracht unendlich vieler Primzahlen kann auch jedes
fernste Intervall so groß gewählt werden, daß hinreichend viele Primzahlabstände für die Funktion
rh(n) vorhanden sind. Die Folge ist: Alle
Primzahlabstände, auch Primzahlzwillinge mit
a=2, kommen in
jedem nächsten, höheren Intervall immer
wieder in
der bekannten, konstanten Häufigkeitsrelation vor. |
