Zur Erinnerung... Die Funktion der relativen Häufigkeit der Primzahlabstände lautet:
rh(n) ~ M0 * (f1-1)/(f1-2) *
(f2-1)/(f2-2) *..... (fk-1)/(fk-2)
M0
Grundmenge ( = Menge der Primzahlzwillinge, auch
pi.a2 )
f_ ungerade
Primfaktoren des Primzahlabstandes
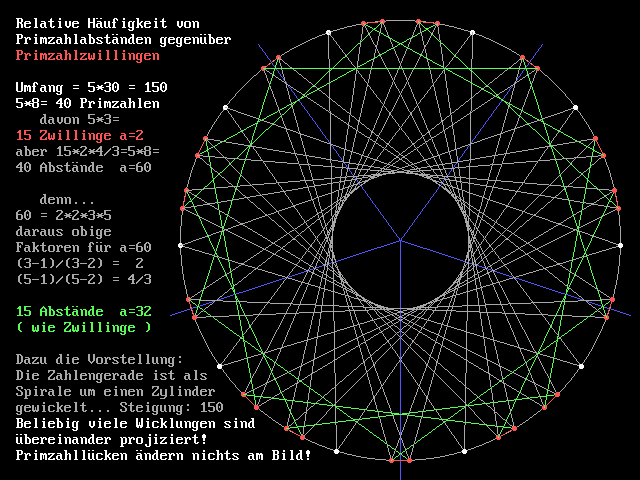
Das Bild ist durch den
enthaltenen Text fast
selbsterklärend. Nur die beiden letzten Sätze
sollten ergänzt werden. Stellt man sich die Wendel
durchsichtig vor, dann erscheinen alle Primzahlplätze besetzt,
selbst dann, wenn ein
betrachtetes, 'tatsächliches' Intervall beliebige
Primzahllücken aufweist. Oder, man stelle sich vor, der
Schnitt zeigt alle möglichen Primzahlplätze die nach der
Eratosthenes-Streichung (2,3,5) übrig geblieben sind..., siehe
oben.
In dieser Darstellung modulo 150 (=5*30) ist die 'gegebene' Anzahl der Zwillinge 15 (=5*3). Dieser Wert ist hier - und nur hier - jene Grundmenge M0 für alle anderen Abstände, die die Primfaktoren 2, 3, 5 besitzen.
Anmerkung: Statt 5*30 hätte auch jedes andere Vielfache von 30 verwendet werden können, auch 7*30, obwohl das eventuell zu Fehlschlüßen verleiten könnte, da 7 die nächstfolgende Primzahl ist. Primzahlen gleich oder größer 7 sind hier nicht berücksichtigt.
Generell siehe: Konzentrat: "Relative Häufigkeit von Primzahlabständen"
In dieser Darstellung modulo 150 (=5*30) ist die 'gegebene' Anzahl der Zwillinge 15 (=5*3). Dieser Wert ist hier - und nur hier - jene Grundmenge M0 für alle anderen Abstände, die die Primfaktoren 2, 3, 5 besitzen.
Anmerkung: Statt 5*30 hätte auch jedes andere Vielfache von 30 verwendet werden können, auch 7*30, obwohl das eventuell zu Fehlschlüßen verleiten könnte, da 7 die nächstfolgende Primzahl ist. Primzahlen gleich oder größer 7 sind hier nicht berücksichtigt.
Generell siehe: Konzentrat: "Relative Häufigkeit von Primzahlabständen"
