Bei meinen Ganzzahl-Knobeleien warte ich seit vielen Jahren auf eine korrekte Antwort zu dem aufgeworfenen Sechseck-Problem. Bisher ist es eine absolute Fehlanzeige! Natürlich kam der Vorschlag per Rechner einen brachialen Suchlauf zu starten, aber man erkannte selbst, daß dies nicht die Antwort auf die gestellte Geometriefrage sein konnte. - Nun ist der Feuerbachsche Kreis nicht gerade tägliches Schulbrot. Er wird gelegentlich auch unter dem Namen Poncelet-Kreis gehandelt, aber genau so selten. Noch nie fand ich eine Verknüpfung von Feuerbach und Primzahlen! Und doch ist das Thema sehr interessant, deshalb löse ich hier und heute in 2004 die im Jahre 1998 gestellte kleine Rätselfrage!

Zunächst aus dem Brockhaus von 1968:

"Der Feuerbachsche Kreis geht durch die Seitenmitten eines Dreiecks, die Höhenfußpunkte und die Mitten der von den Ecken ausgehenden Höhenabschnitte. Der F. K. berührt den Inkreis und die drei Ankreise des Dreiecks. Sein Mittelpunkt liegt auf der Eulerschen Geraden des Dreiecks, und sein Radius ist gleich dem halben Umkreisradius."

Diesen Text möchte ich ergänzen mit:

"Wählt man für den Radius des Feuerbachschen- oder Neunpunktekreises das Quadrat einer Trimzahl (Trimzahlen - Untermenge der Primzahlen), dann ist jeder beliebige Abstand eines der 9 Punkte zu einem der 8 anderen Punkte ganzzahlig, also das Produkt von "kleinen Primzahlen". Anmerkung: Als Trimzahl gilt hier auch das Produkt von Trimzahlen."

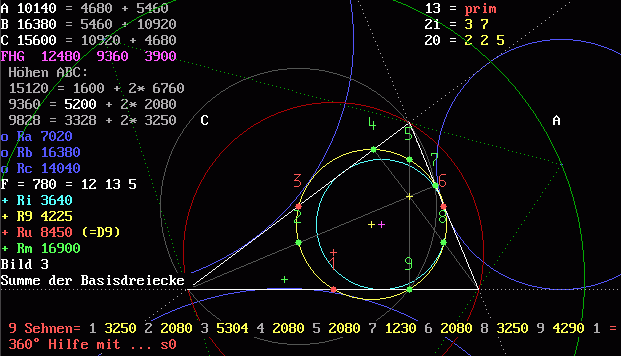
Gehen wir direkt in die Vollen mit einem Arbeitsbild aus einem Programm zu diesem Thema. Es bearbeitet beliebige Dreiecke, in denen Seiten, Radien und diverse Punktabstände ganzzahlig gewählt werden können. Dazu gehören auch die Abstände der 9 Punkte im Feuerbachschen Kreis. Basis der Figur im Bild ist das schiefwinkelige Dreieck 13_21_20, das bei einer Erweiterung mit 780 das Dreieck 19140_16380_15600 liefert. Letzteres hat dann einen Neunpunktekreis mit dem Radius R9 = 4225 = (5*13)^2. In der vorletzten Zeile des Bildes sind die 9 ganzzahligen Sehnen zwischen den Punkten 1 bis 9 in Folge angegeben. Es ist zu beachten, daß die Reihenfolge der Punkte bei 6 und 7 in diesem Beispiel wechselt. Will man nun statt 9 gezielt nur 6 Punkte auf dem gelben Kreis mit dem Radius R9 haben, kann man völlig beliebig 6 Punkte (rot oder grün) wählen. Ihre Abstände werden immer ganzzahlige Werte haben! Die 6 Punkte sind dann die Ecken eines unregelmäßigen Sechsecks und liegen auf dem Radius R9 = 4225. Soweit zur Lösung der alten Aufgabe.

Oben 9 ganzzahlige Abstände
Unten 6 ganzzahlige Abstände, z.B.:

Doch wo sind die zugehörigen kleinen Primzahlen geblieben? Sehen wir uns die Primzahlfaktoren der 6 Feuerbach-Sehnen an und stellen fest, nicht alle Sehnen haben den Faktor 13 (!) :

3250=2*5*5*5*13   2080=2*2*2*2*2*5*13   7800=2*2*2*3*5*5*13
1230=2*3*5*41     5070=2*3*5*13*13      4290=2*3*5*11*13

Der verehrte Mathematiklehrer Feuerbach würde seine Freude daran haben! Ich hoffe, Sie auch.

Für Sie, den Leser einer Homepage, noch ein Brückenschlag zu Kreise im Kreis - mit kleinen Primzahlen. Das folgende Bild zeigt - ähnlich wie oben - ein Basisdreieck 13_14_15, das ebenfalls zu erweitern ist. Hier ist der grüne Inkreis fast gleich dem gelben Feuerbach-Kreis, da die Seiten des Dreiecks nur um den Wert 1 differieren. Das Bild zeigt, daß auch über das schiefwinkelige Dreieck ohne Inversion für den Inkreis der Eckenkreise, den Umkreis der Eckenkreise (beide weiß) und die drei Eckenkreise (lila) ganzzahlige Werte zu finden sind! Die 5 Kreise tangieren in 9 Punkten, ohne Bezug zu Feuerbach.

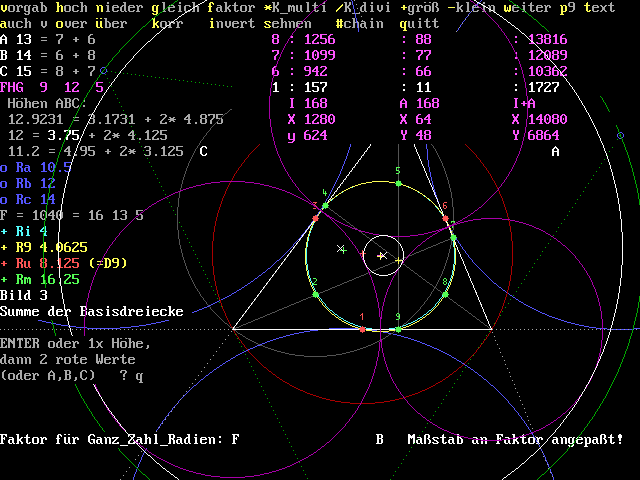
Hierzu nach Erweiterung mit 1040:
Zu beachten ist, einige Sehnen entsprechen jenen des ersten Bildes!

Der Trick der vielfachen Ganzzahligkeit in schiefwinkeligen Dreiecken liegt natürlich wieder beim Satz des Pythagoras. In beiden obigen Bildern trennt die Höhenlinie auf den Fußpunkt 9 das schiefwinkelige Dreieck in je zwei pythagoräische Dreiecke. Nur wenn diese Bedingung erfüllt ist, findet man den Weg zu den ganzen Zahlen, zu den Primzahlen... bei schiefen Winkeln und dem Neunpunktekreis. In beiden Fällen bezw. Bildern basiert die linke Dreiecksseite C auf der 5 und die rechte Seite A auf 13, den beiden kleinsten Trimzahlen. In beiden Fällen hat nach der richtigen Erweiterung der Feuerbachsche Kreis den Radius R9 = (5*13)^2 = 4225. - Dagegen ist für die Ganzzahligkeit der genannten 5 Kreise mit 157 bezw. 11 zu erweitern!