Hierzu siehe auch die Ergänzung: DreiecksInkreise & EckenKreise

Meine Homepage titelt: "primini"... und das Produkt der vier kleinsten Primzahlen ist 210.
( 210 ...   Auch eine wichtige Zahl nach DIN, doch dazu am Ende des zweiten Teiles dieser Seite. )
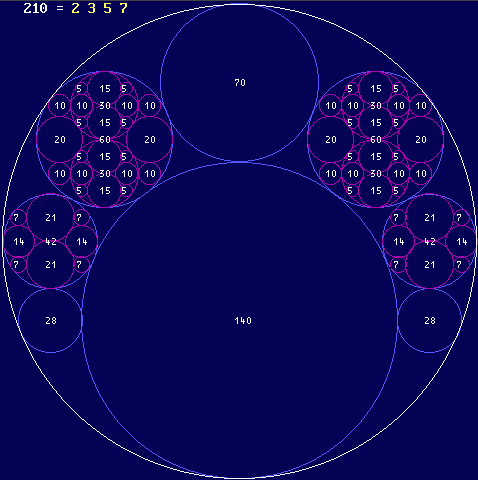
Zeichnet man einen Kreis mit dem Radius 210 und versucht ganzzahlige Kreise symmetrisch und tangierend einzutragen, ergibt sich schon ein nettes Bildchen mit 72 kleineren Kreisen im Außenkreis, das man so nicht erwartet hätte. Wichtig:

Alle Radien (weiße Zahlen) und alle Koordinaten der Kreismittelpunkte sind ganzzahlig.

Getreu meinem Motto ohne Formeln auszukommen, nehmen wir die drei Radien der blauen Kreise 28_42_140, ihre Summe ist r=210. Kürzen wir die Radien durch 14, finden wir 2_3_10. Die Teilsummen dieser Werte führen zu dem pythagoreischen Dreieck 5_12_13.... Nebenbei: Die Orte der Zahlen 28_42_140 sind die Eckpunkte dieses Dreiecks.
Die lila (magenta) Kreise sind 7_14_21. Gekürzt durch 7 finden wir 1_2_3 und das Dreieck aller Dreiecke 3_4_5....

Die nächste Primzahl wäre die 11. Multipliziren wir den bisherigen Außenradius von oben mit 11 (=2310) und versuchen wieder möglichst viele Kreise rekursiv und ganzzahlig unterzubringen, sind es schon 488 tangierende Gesellen.

Doch die Auflösung unserer Grafik reicht nicht mehr aus. Zoomen wir die linke obere Ecke, erhalten wir einen kleinen Zipfel der unendlichen Möglichkeiten, die uns unsere "kleinen Primzahlen" eröffnen. Suchen Sie bitte oben links... 110, 110, 330 und darüber 165. Im folgenden Bild stehen diese vier Zahlen am unteren und rechten Bildrand:

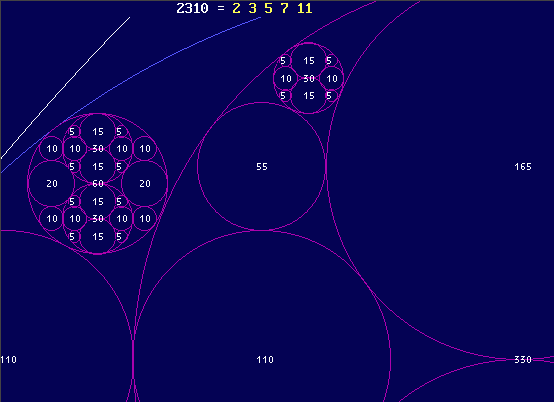
Zum Abschluß noch ein beliebig gewähltes Datum: Ein Kreis mit einem Radius von R=69300 (=2x2x3x3x5x5x7x11) nimmt nach diesem Spiel mindestens 218784 ganzzahlige Kreise auf. Darüber hinaus bestünden für dieses R weitere Möglichkeiten mit anderen ganzzahligen Dreiecken. Viel Spaß, falls Sie meinen Spuren folgen sollten.....

Der Titel scheint etwas weit hergeholt. Dem ist aber nicht so!

Als die Väter der Normen die Papierformate in Angriff nahmen, machten sie eine klare, einfache Vorgabe. Die DIN-Reihe A sollte ausgehen von einem Bogen, der eine Fläche von 1 m² besitzt. Unhandlich wäre ein Bogen von 1 m x 1 m gewesen. Statt dessen wählte man ein Seitenverhältnis von 1 : Wurzel(2) und jeder nächst kleinere Bogen sollte immer die Hälfte des größeren sein. Für DIN A0 ergab sich somit:

a * a * Wurzel(2) = 10^6 mm²         a = Wurzel(10^6 / Wurzel(2)) = 840.896

Gerundet legte man fest:   841 x 1189 mm

Details wieder bei Jürgen Köller http://www.mathematische-basteleien.de/, Titel DIN.

Das Produkt der beiden Zahlen mußte nahe 10^6 liegen und das Verhältnis der Zahlen mußte eine gute Approximation für die Wurzel(2) sein. Zerlegt man beide in Primfaktoren, wird es interessant:

841 x 1189 = 999949

841 = 29 x 29   und    1189 = 29 x 41

Interessant deshalb, da 41 / 29 eine sehr gute Näherung für die Wurzel aus 2 ist, die schon die Urväter der Mathematik kannten! Beinahe zwangsläufig mußte sie hier auftauchen. - Und nun zu den kleineren DIN-Formaten, die durch halbieren entstehen. Kluger Weise rundete man nach der Halbierung ab. Statt 420.5 x 594.5 wählte man 420 x 594, was zu 210 x 297 führte. Wieder sind die Primfaktoren dieser Zahlen bemerkenswert: 210 = 2 x 3 x 5 x 7 und 297 = 3 x 3 x 3 x 11 = 3 x 99, Insbesondere wichtig ist ... 99, siehe folgende Grafik:

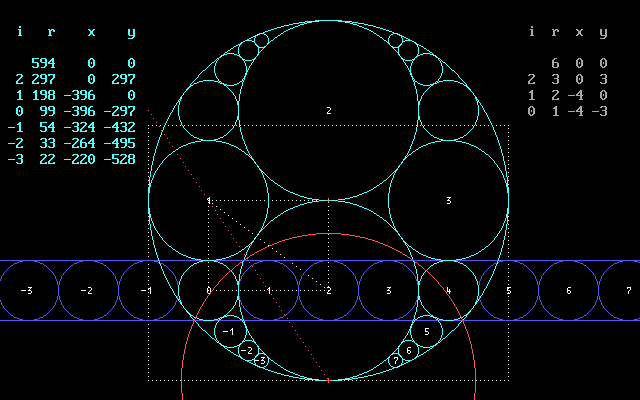
Was zeigt das Bild?

Generelle Darstellung einer Inversion (Spiegelung an einem Kreis):
Alle blauen Elemente - Kreise und Geraden - werden am roten Kreis gespiegelt und liefern so die Kreise in türkis !!!

Spezieller Fall:
Das große Rechteck ist DIN A0 mit 841 x 1189.
Der große Kreis hat einen Radius von 594, das wichtige DIN-Maß.
Die zwei Dreiecke haben die Basis 3_4_5 und erweitert mit 99 die Seiten 297_396_495. Diese Erweiterung führt dazu, daß alle gezeigten Kreise und deren Koordinaten ganzzahlig sind, Tabelle links oben! Ohne Erweiterung sind nur die Kreise 0 bis 4 ganzzahlig, Tabelle rechts oben. Beim Kreis 1 ist der Spiegelstrahl eingetragen, auf dem die Kreis-Schnittpunkte (nicht die Zentren!) maßgeblich sind. Wichtig: Der Radius des Spiegelkreises ist so zu wählen, dass dieser den Dreieck-Eckenkreis (r0=1) rechtwinkelig schneidet! Rot geht somit nicht durch das Zentrum von 0.
Für das Dreieck 3_4_5 ist hier der Radius rs des Spiegelkreises:

Rs = wurzel(5²-1²) = Wurzel(24)   ....   und für den DIN-Fall wieder zu erweitern mit 99.
Tatsächlich gebraucht wird die Wurzel nicht, sondern nur     Rs² = 24    (siehe auch unten)

Purer Zufall ist, daß die Primfaktoren von 594 die Werte 3² und 11 enthalten. Nur so entstehen die herrlichen Kreise im Kreis nach DIN !!! Millionenfach wurden im letzten Jahrhundert DIN A0 und alle Halbbrüder eingesetzt. Ich frage meine Kollegen - die Herren Konstrukteure - kannte oder kennt einer diesen ganzzahligen Spaß der 21 Kreise nach "DIN"? - Nie gehört!

Auflösung des obersten Bildes dieser Seite:

Ein Kreis mit r=210 (Durchmesser 420) passt exakt auf ein Blatt DIN A2.
Die beiden untersten Kreise haben einen Radius r=28. Setzen Sie zwischen diese beiden 5 weitere 28-er Kreise, also nebeneinander auf einer Geraden in den 140-er Kreis. Diese 5 Kreise liefern auch hier bei inverser Abbildung die oberen Kreise 42_60_70_60_42 !!!

Querverweis zu Trimzahlen (Tripel) Dort findet man die Folge A... hier solo angewandt! Das sind ganzzahlige Dreiecke mit einem ungeraden a (>1) und c,b = a²/2 ±0.5. Wählt man diese Dreiecke, dann ist die Anzahl der kleinen Eckenkreise im größten Eckenkreis gleich dem Zahlenwert der Gegenkathete b.

Beim obersten  Bild war es das Dreieck 5_12_13... daher 5 Kreise.
Beim untersten Bild war es das Dreieck 3_4_5...... daher 3 Kreise.
Und so wären es etwa bei dem Dreieck 19_180_181..... 19 Kreise. Das liest sich fast wie ein Scherz, den man mit etwas Mathe jedoch leicht nachprüfen kann!

Nachprüfbar ist bei all den Integer-Kreisen: Immer liegen die Mitten zweier tangierenden Kreise auf den Eckpunkten ganzzahliger Dreiecke. Die Kreismitten der großen DIN-Figur bilden ein raffiniert verwobenes Netz ganzzahlig, rechtwinkeliger Dreiecke!

2 Hinweise zur Programmierung ganzzahliger Kreise ... Trick 1:
Im ersten Schritt werden bei der Inversion alle Radien und Koordinaten konsequent durch ganzzahlige Brüche ausgedrückt. Eine X_Koordinate lautet dann immer X_Zähler/X_Nenner. Will man anschließend eine bestimmte Anzahl von Radien und deren Koordinaten ganzzahlig haben, dann ist das "kleinste gemeinsame Vielfache" dieser Nenner zu ermitteln und alle Werte entsprechend zu erweitern. Fertig! - Hier noch ein solches Arbeitsbild, bei dem der Koordinaten-Nullpunkt vorteilhaft in das Zentrum des Spiegelkreises verlegt wurde. Wieder zu beachten sind die 7 Kreise des Dreiecks 7_24_25 und die kleinen Primfaktoren der Nenner:

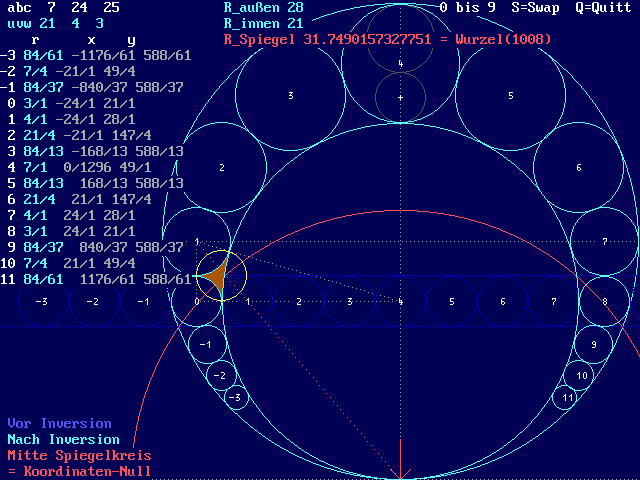
Für die Spiegelung am Kreis (Inversion) benötigt man nur die eine Formel    Rs² = Ev*En    dabei bedeuten:

Rs = Spiegelkreis, wobei von diesem immer nur sein Quadratwert gefragt ist !!!
Ev = Entfernung (zur Mitte des Spiegelkreises) eines zu spiegelnden Punktes vor der Inversion
En = Entfernung (zur Mitte des Spiegelkreises) eines gespiegelten Punktes nach der Inversion
Wichtig bei der Spiegelung eines Kreises: Es sind immer 2 Punkte zu berechnen,...
das sind die 2 Schnittpunkte seines Umfanges mit dem Spiegelstrahl !!!

... Trick 2, im Bild gelb markiert:
In jedem Dreieck bezw. dem ergänzten Rechteck sind die 4 Eckpunkte die Mitten von 4 tangierenden Kreisen (gilt abgewandelt auch für schiefwinkelige Dreiecke). Die 4 Kreise sind die 3 Eckenkreise und der diese umschließende Umkreis! Achtung: Der kleinste Eckenkreis (beim rechten Winkel) ist deckungsgleich dem Inkreis des Dreieckes, hier gelb markiert. Benutzt man nun den Inkreis als Spiegelkreis, dann wird der gespiegelte Umkreis zu einem kleinen, zentralen Kreis, der die 3 Eckenkreise tangiert! Dies alles passiert in dem markierten Feld, das ich "Zwickel" nenne. Theoretisch kann man auf diese Art für jeden "Zwickel" obiger Bilder den zugehörigen, auch ganzzahligen Inkreis der 3 Eckenkreise finden. Dazu eine spezielle Basisinformation: DreiecksInkreise & EckenKreise