Will man das Kreisthema voll durchblicken, sollte man die geometrische Basis des spannenden Problems studieren. Wie schon beschrieben, geht das Tangieren der ganzzahligen Kreise immer wieder auf ganzzahlige Dreiecke zurück. Das heißt aber nicht, daß man diese Dreiecke mühsam finden und berechnen muß. Repräsentant des Dreiecks ist sein Inkreis! Die hier verwendete Inversion macht das gewissermaßen mit "links". - Spezielle "Links ", im Sinne von Adressen im Netz, wird man dazu allerdings kaum finden!

Der entscheidende Ansatz, den man in den nächsten Bildern studieren kann, lautet:

In jedem Dreieck schneidet der Inkreis die drei Eckenkreise unter 90° !!
(Von Bedeutung mit der sogenannten "Winkeltreue" der Inversion.)

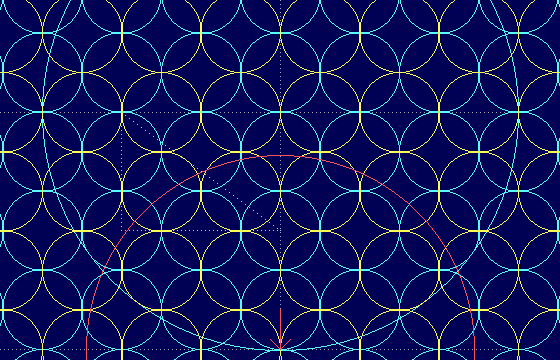
Die Grafik zeigt geordnete Kreise in der Ebene mit einem Einheitsradius, hier ri=1 beim Dreieck 3_4_5. Die eine Farbe (gelb) stellt die Inkreise dar, die andere den jeweils kleinsten Eckenkreis, wobei diese Gruppen von Kreisen gleich, jedoch in Richtung x und y gegeneinander um 1 verschoben sind. Der rote Spiegelkreis schneidet mindestens einen "parkettierten" Kreis jeder Farbe rechtwinkelig, der dann bei der Inversion in sich übergeht, also unverändert bleibt:

Vor der Inversion

Nun verändern wir die Grafikausgabe geringfügig: Jeder der kleinen Kreise wird an dem roten Spiegelkreis "invertiert"! Sieht dann so aus:

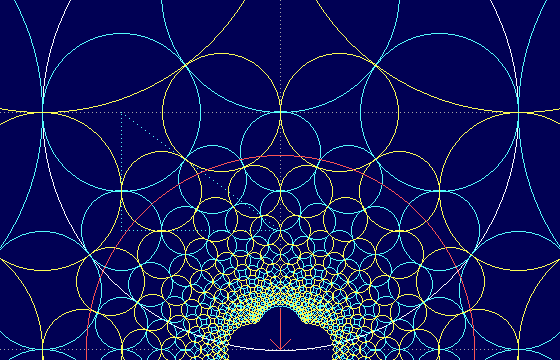
Nach der Inversion

Dem aufmerksamen Leser wird nicht entgehen, daß in dem Bild nur der größte Außenkreis (weiß) eingetragen ist. Die anderen neuen, jeweils kleineren Außenkreise hätten das Bild hier nur zerstört. - Auf der Seite Kreise im Kreis - mit kleinen Primzahlen erläuterte ich, wie man in jeden "Zwickel" einen weiteren ganzzahligen Kreis tangierend einsetzen kann. Nun hat man dafür - ohne das Dreieck genau zu kennen - mit jedem gelben Kreis einen Dreiecksinkreis zur Verfügung. Benutzt man einen der gelben Kreise als neuen Spiegelkreis und spiegelt den zugehörigen Außenkreis nach innen, hat man einen neuen kleinen "Inkreis".... Nebenbei: Die 3 (4) benachbarten Kreise (türkis) werden dabei nicht invertiert, sie werden ja senkrecht von gelb geschnitten!!!

Viel Spaß bei der (Primzahl-) Faktoren-Analyse der 1000 Kreise!
Hier sind die Werte, diesmal für die Radien der gelben Inkreise:

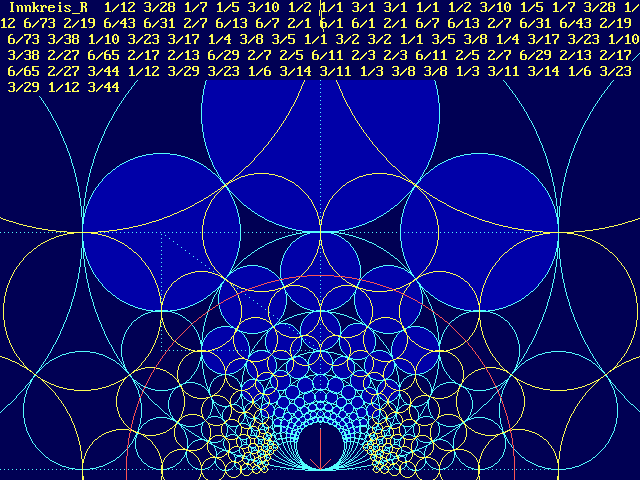
Ein Punkt ist noch von Bedeutung: Der Bildaufbau startet mit dem Dreieck 3_4_5. Das Resultat ist, wie bereits besprochen, daß ab Kreismitte nach oben 3 Kreise (blau) vorhanden sind. Im nächst kleineren Kreis, der gefüllt wird, sind es ab Kreismitte 5 blaue Kreise, dann 7, 9,... usw., exakt der genannten Dreiecksfolge A entsprechend.

Im obigen Bild sind gelbe und türkise Kreise beide entstanden aus konstant großen Kreisen, die dem Dreiecks-Inkreis entsprechen. Wählt man nur für gelb als Ausgang vor der Inversion statt ri ein r=ri*(wurzel(2)-1) ergibt sich eine nette Variante im nächsten Bild: Jeder gelbe Vollkreis tangiert exakt die 4 benachbarten türkisen Kreise! Jeder türkise Kreis tangiert dagegen 8 andere Genossen. Ein Wermutstropfen ist allerdings dabei. Die gelben Radien sind nicht mehr als ganzzahlige Brüche auszuweisen. Die Wurzel aus 2 verdirbt das Spiel:

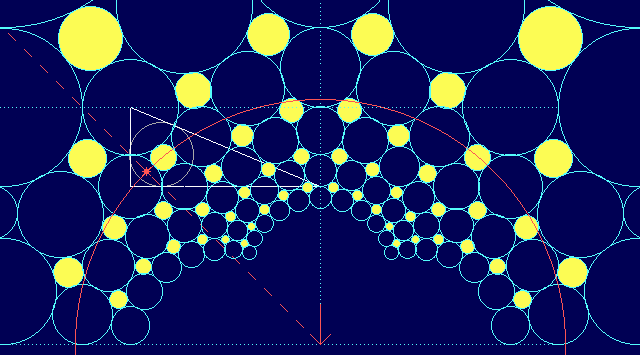
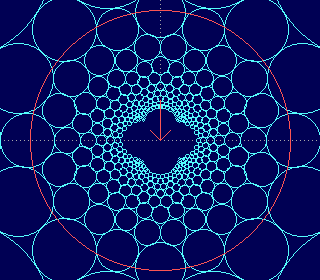
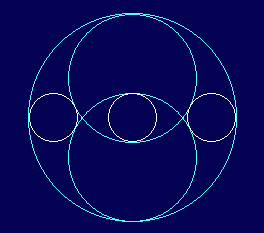
Als kleines Rätsel sollen die zwei letzten Bilder gelten. Zwei verschiedene Wurzeln verhindern hier teilweise die Ganzzahligkeit! Welche? - Nun das linke Bild zeigt viele gleich große Kreise, die vor der Inversion die Ebene in der dichtest möglichen Packung füllen. - Das rechte Bild nenne ich "Harmonie". Es könnte auch über ein spezielles Dreieck mit dem Kathetenverhältnis 1:2 und der Inversion gewonnen werden. Die 3 weißen Kreise sind gleich groß!
Also: Welche Wurzel stört in welchem Bild?

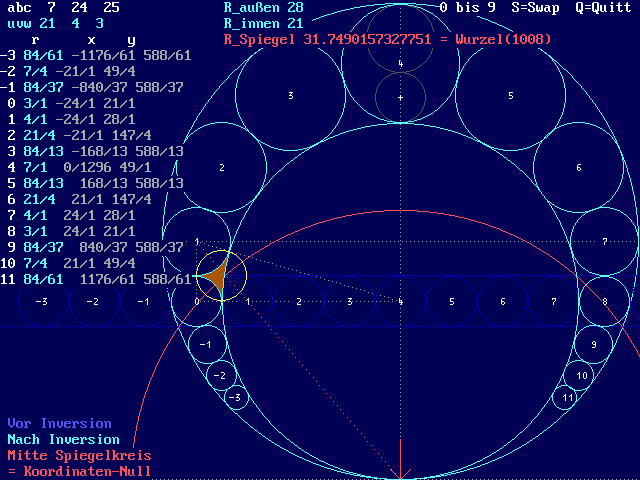
Bei solchen Inversionen ist es oft schwierig zu erkennen, welcher Kreis wohin gespiegelt wurde. Ich möchte dies an einem scheinbar einfachen Beispiel erläutern. Das blaue Muster im Hintergrund zeigt die Kreise vor der Inversion, mit den Radien R=1, 2, 3 (von Dreieck 3_4_5). Grau hinterlegt sind die Kreise 0 bis 27, nur mit den Radien R=1, 2, 1, 2, .... von unten nach oben.
Nach der Inversion sind es die grünen Kreise, wieder 0 bis 27. Dazu die Tabelle ganzzahligen Brüche für Radien und X-Y-Koordinaten !!
Hätten Sie dies auf Anhieb zeigen können?

Gegen mein eigenes Prinzip einer formelarmen Homepage ...
... einige Formeln zur Inversion - gekoppelt an pythagoräische Tripel:

Die Spiegelung am Kreis gehört meist nicht zum Handwerkszeug des Hobbyprogrammierers. Dabei sind es nur wenige einfache Ausdrücke, mit denen man die besonderen Effekte der Inversion nutzen kann. - Zu den Tripel sagen die meisten Mathematiker spöttisch: "Da ist nichts mehr zu holen!" - Jedoch, die Medaille hat 2 Seiten, die zweite ist die Inversion, die erste Seite sind die alten, ganzzahligen Dreiecke, die wir uns als Start über m und n holen können:

a=m²-n²   b=2*m*n   c=m²+n²   Inkreis(=kleinster Eckenkreis):   ri=n*(m-n)

Wir bilden ein horizontal liegendes Rechteck, in dem wir zwei dieser Dreiecke an der Hypotenuse zusammenfügen. Die rechte obere Ecke soll Mitte der Kreisfigur mit dem Außenradius ra sein. An den anderen 3 Ecken werden die 3 Eckenkreise u, v und w als Inkreise zu ra eingetragen. Am tiefsten Punkt tangieren ra und u. Dieser Punkt ist Mitte Spiegelkreis. Ausgehend von dem rechten Winkel des Dreiecks (linker unterer Rechteckpunkt) können weitere Kreise in waagrechter Reihe oder als "Parkett" angeordnet werden.

Eckenkreise     u = n*(m+n)   v = m*(m-n)   w = n*(m-n) = Inkreis
ra   Außenkreis     ra = c+w = u+v+w

Soll der Inkreis und w unter 90° vom Inversionskreis geschnitten werden,
findet man dazu das Quadrat des Spiegelkreis-Radius  rs:

rs^2 = 4 * m * (m+n) * n^2
für das Dreieck 3_4_5 mit m=2 und n=1 wird rs^2=24

Bei der Inversion gilt.... herausgegriffen und etwas verkürzt:

• Jeder Kreis, der nicht durch den Mittelpunkt des Spiegelkreises geht, liefert gespiegelt stets wieder einen Kreis.

• Zur Spiegelung eines Kreises kann nicht einfach sein Mittelpunkt benutzt werden. Vielmehr sind 2 diametral gegenüberliegende Punkte des Kreises zu invertieren. Erst aus diesen Daten ergeben sich die Werte für den gesuchten Kreis und seinen Mittelpunkt. Die dafür notwendigen Schritte sind hier zusammengefaßt (ohne Ableitung):

Es bezeichnen:

rs   Spiegelkreis, seine Mitte ist Koordinaten-Null
rsq = rs²   Quadrat des Spiegelkreises, nur dieses wird benötigt
r1   Radius eines Kreises vor der Spiegelung
r2   Radius eines Kreises nach der Spiegelung
z1,z2   allgemein, Punktentfernungen vor und nach Spiegelung
x1,y1   Mittelpunkts-Koordinaten eines Kreises vor der Spiegelung
x2,y2   Mittelpunkts-Koordinaten eines Kreises nach der Spiegelung

rsq   siehe oben oder über die xy-Koordinaten des mit 90° zu schneidenden Kreises....
rsq = x^2 + y^2 - ri^2

Allgemein gilt für Inversion:     rsq = rs^2 = z1*z2

Speziell für den Kreis:

r2 = r1 * rsq / (x1^2 + y1^2 - r1^2)

x2 = x1 * r2 / r1
y2 = y1 * r2 / r1

Die erhaltenen Werte für x2, y2 und r2 genügen zur Erstellung einer Grafik. Will man dagegen die numerischen Angaben für ganzzahlige Brüche - Zähler und Nenner - haben, empfiehlt sich folgender Weg...

r2z   Zähler von r2
x2z   Zähler von x2
y2z   Zähler von y2
nn   Nenner zu r2z, x2z und y2z

Zähler:      r2z = r1*rsq     x2z = x1*rsq     y2z = y1*rsq
Nenner:     nn = x1^2+y1^2-r1^2

Eventuell wieder zurück zur Seite:     Kreise im Kreis - mit kleinen Primzahlen