
|
Primzahlabstände: Sinnvolle Intervalle Programmtechnik - Download |
|
Programmtechnik - Download |
|
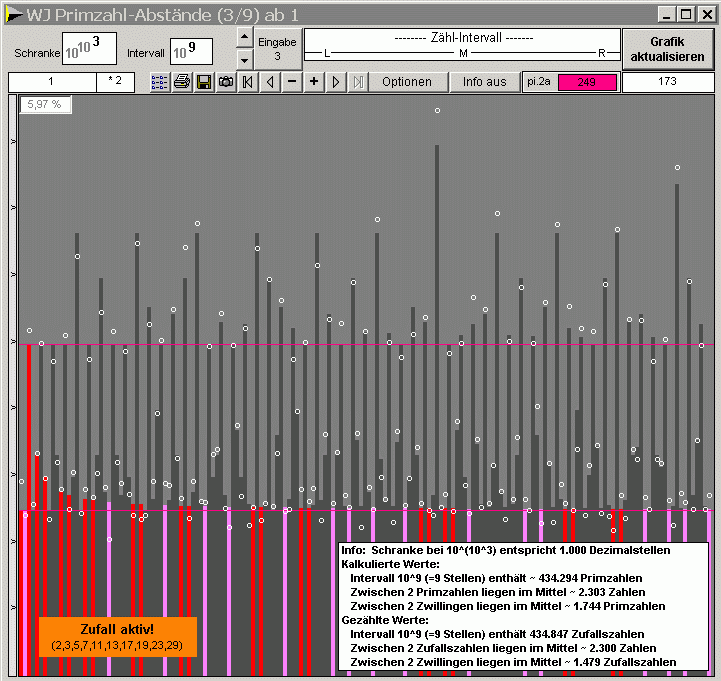
Die
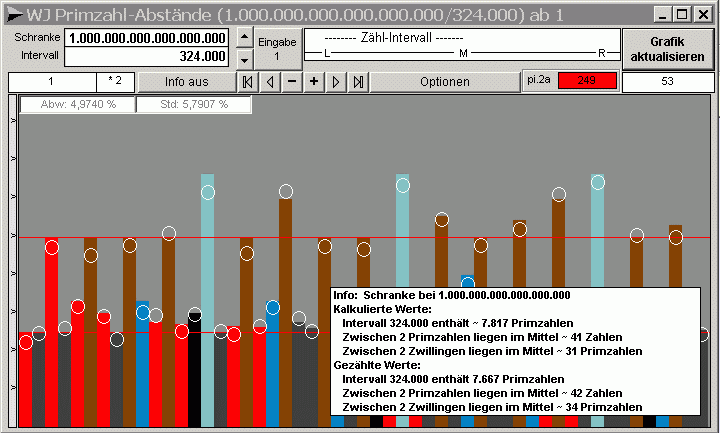
Schranke liegt bei 1.000
Dezimalstellen und das Intervall ist 1 Milliarde groß....
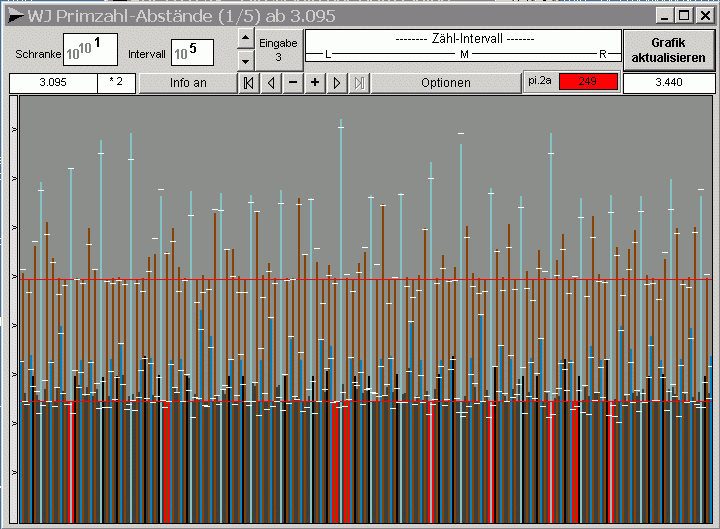
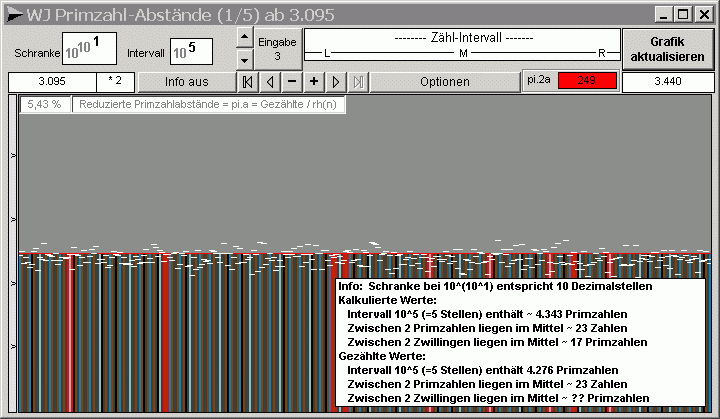
Bei dieser Simulation wurden statt echter Primzahlen sogenannte Zufallsprimzahlen eingesetzt. Diese erfüllen allerdings die wichtige Bedingung, daß sie nicht durch die Primzahlen 2 bis 29 teilbar sind. Als Ergebnis zeigt die Grafik, die Häufigkeit von Primzahlabständen in Abhängigkeit von den Primfaktoren der Abstände, unabhängig davon, ob echte oder Zufallsprimzahlen eingesetzt werden. Überwiegend bestimmend ist das mod_ 30_Muster der kleinen Primzahlen 2, 3 und 5... hier ergänzt durch die Faktoren 7 bis 29. Eine solche Parkettierung entspricht der natürlichen Prägung des unendlichen Zahlenstrahls.... bis an sein nicht existierendes Ende. Selbstverständlich ist die Anzahl dieser gezählten Abstände und auch der Zwillinge eine Näherung - aber eine sehr gute! Tatsächliche Auszählungen und deren Simulation durch (Pseudo-) oder Zufallsprimzahlen zeigen eine äußerst gute Übereinstimmung der Werte für die 'relative Häufigkeit von Primzahlabständen' - auch in sehr hohen Bereichen. Je besser (...der Natur nachgebildet!) die unendliche Zahlengerade 'primorial' (=Produkt der Primzahlen kleinergleich n) parkettiert ist, desto besser das Resultat. Eine verwendete Parkettierung sollte daher möglichst nicht nur mit den wichtigen Faktoren 2, 3 und 5 erfolgen. Die Software gestattet eine entspechende, wahlweise Einstellung! Daß bei einer Schranke gegen unendlich auch das Intervall zu einer unvorstellbaren Größe wird, muß klar erkannt werden. Für jede abzählbare Größe und Übergröße gelten jedoch die hier aufgezeigten Zusamenhänge zwischen Primzahlen, Primzahlzwillingen und Primzahlabständen, scheinbar chaotisch und doch streng geordnet.... Und, vergessen wir nicht: ►► Jede Computer-Grafik bleibt im Endlichen. Sie kann jedoch als gedankliche Brücke dienen. ◄◄ |