10^(10^1) oder 10^(10^10) oder 10^(10^100)
Man sollte über die eigene Kühnheit erschrecken. Es ist einfach dreist und für den täglichen Zahlengebrauch vollkommen überzogen. Denn die mittlere Zahl (Schranke) hat bereits 10 Milliarden Stellen. Und die dritte Zahl? Nicht nur, daß man sich diese Zahl selbst nicht vorstellen kann, nein, allein ihre Stellenzahl ist mit 10^100 außerhalb unserer Maße!
Dennoch läßt sich relativ einfach anschreiben, wie es um Primzahlen, Primzahlzwillinge und Primzahlabstände in diesen hohen Bereichen bestellt ist. Genau das ist mein Thema. Wir wissen um die Tatsache jener 'unendlich' vielen Primzahlen, die in hohen Bereichen existieren - nicht nur in der Theorie. Und daß unser Zählen bei 10^(10^100) noch meilenweit von unendlich entfernt ist, das sollten wir niemals vergessen. ( Eingefügt sei hier: Die derzeit größten, bekannten Primzahlen haben 'nur' 10^7 also10 Millionen Stellen... ) Trotz alledem, für die mittlere Zahl 10^(10^10) mit 10 Milliarden Stellen gilt ohne jeden Kompromiß:
Zwischen zwei
Primzahlen liegen im Mittel ~ 23 Milliarden Zahlen.
Zwischen zwei Primzahlzwillingen liegen im Mittel ~ 17 Milliarden Primzahlen
und ein Intervall an dieser Stelle, das ~250 Zwillinge enthält,
hat 23 Dezimalstellen mit... ~4.343 Milliarden Primzahlen.
Das alles steht in der unteren Tabelle (untere Hälfte) in Zeile 10.
Zwischen zwei Primzahlzwillingen liegen im Mittel ~ 17 Milliarden Primzahlen
und ein Intervall an dieser Stelle, das ~250 Zwillinge enthält,
hat 23 Dezimalstellen mit... ~4.343 Milliarden Primzahlen.
Das alles steht in der unteren Tabelle (untere Hälfte) in Zeile 10.
Diese Werte muß man erstmal
aufnehmen. Nur
allzu verständlich ist, wenn selbst
Mathematiker gelegentlich schreiben: Wir wissen heute nicht, ob in
diesen Extrembereichen überhaupt noch Primzahlzwillinge
anzutreffen sind. Wir nehmen es an, beweisen konnte man es
bisher nicht (2005).
Das
ist der Tenor. Aber
solche
Zweifel sind vollkommen fehl am Platze.
Meine
Bemühungen gehen deshalb dahin, meinen Lesern Erkenntnisse zu
vermitteln, die in jedem fernsten Bereich Gültigkeit haben. Und
schockierend schreibe ich hier in dieser laufenden Zeile: Es gibt in
diesem Sinne kein
Unendlich, nicht in unserem und auch keinem anderen Zahlensystem. Immer
kann eine neue (10er-) Potenz oder ein weiterer Faktor für
ein nächstes Produkt eingesetzt werden. Dieses Verfahren ist
ohne Ende. Wir befinden uns gedanklich im 'abzählbar'
Unendlichen... und das ist genau jener Bereich in dem die bekannten
Unendlichkeitsbeweise geführt werden.
Die folgende Tabelle soll eine Vorstellung verschaffen zu den Begriffen:
Schranke - Intervall - Anzahl von... Primzahlen, Primzahlzwillingen und Primzahlabständen...
( Die Tabelle enthält Tatsachen und soll den Leser anregen, sich eine eigene Vorstellung zu verschaffen. )
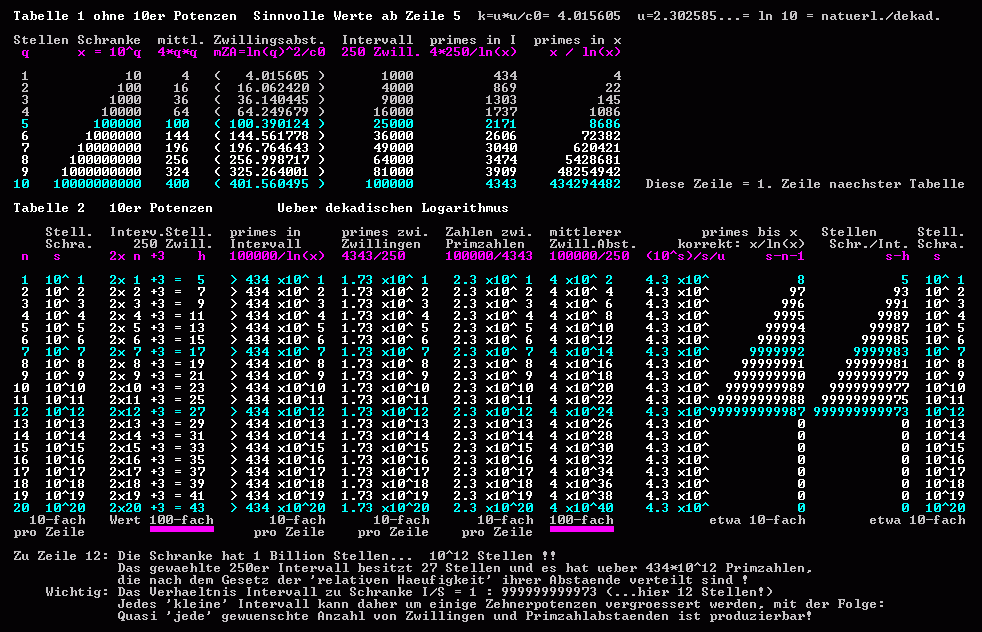
Interessant sind viele Einzelheiten, bitte befassen Sie sich mit diesen ungewohnten Daten !
Z. B. in Zeile 7... eine Zahl mit 10 Millionen Stellen. Wie oben gesagt, dort liegen in 2007 unsere bis dato erreichten Primzahlrekorde. Bis zu diesem Punkt gibt es 4.3 x 10 hoch 9.999.992 Primzahlen.
Und in Zeile 8 ? Die bisherige Gesamtzahl der Primzahlen (aus Zeile 7) hat sich grob verzehntfacht. - Das muß man verarbeiten. Denn jeder spricht von der spärlichen Anzahl von Primzahlen in diesen hohen Bereichen. Man sollte sich aber immer vor Augen halten, was das Anhängen einer einzigen Null bei diesen Stellenzahlen tatsächlich bedeutet: Jede nächstfolgende Potenz führt zu einer weiteren Explosion!
Letzte Spalte:
Man muß erkennen, wie 'klein' ein gewähltes Intervall für ~250 Primzahzwillinge ist... Es ist klein gegenüber der Schranke! Nochmals:
In der 12. Zeile - in dem 'großen' Intervall (= kleiner Bruchteil der Schranke) - sind bereits ~ 250 Primzahlzwillinge enthalten. Und das alles, ohne jeden gedanklichen Trick. Es ist gegeben und verborgen in der natürlichen Ordnung der Zahlen. Man muß es mal primitiv hinschreiben - wenn man darüber sprechen will.
Zurück zu: Konzentrat: "Relative Häufigkeit von Primzahlabständen"
Sie lasen bei den 'kleinen Primzahlen' - mit einem Link zu dem kostenlosen Super-Programm:
Primzahlen oder die Magie der Zahlen http://euroware.de von Reinhold Kiebart
Die folgende Tabelle soll eine Vorstellung verschaffen zu den Begriffen:
Schranke - Intervall - Anzahl von... Primzahlen, Primzahlzwillingen und Primzahlabständen...
( Die Tabelle enthält Tatsachen und soll den Leser anregen, sich eine eigene Vorstellung zu verschaffen. )

Interessant sind viele Einzelheiten, bitte befassen Sie sich mit diesen ungewohnten Daten !
Z. B. in Zeile 7... eine Zahl mit 10 Millionen Stellen. Wie oben gesagt, dort liegen in 2007 unsere bis dato erreichten Primzahlrekorde. Bis zu diesem Punkt gibt es 4.3 x 10 hoch 9.999.992 Primzahlen.
Und in Zeile 8 ? Die bisherige Gesamtzahl der Primzahlen (aus Zeile 7) hat sich grob verzehntfacht. - Das muß man verarbeiten. Denn jeder spricht von der spärlichen Anzahl von Primzahlen in diesen hohen Bereichen. Man sollte sich aber immer vor Augen halten, was das Anhängen einer einzigen Null bei diesen Stellenzahlen tatsächlich bedeutet: Jede nächstfolgende Potenz führt zu einer weiteren Explosion!
Letzte Spalte:
Man muß erkennen, wie 'klein' ein gewähltes Intervall für ~250 Primzahzwillinge ist... Es ist klein gegenüber der Schranke! Nochmals:
In der 12. Zeile - in dem 'großen' Intervall (= kleiner Bruchteil der Schranke) - sind bereits ~ 250 Primzahlzwillinge enthalten. Und das alles, ohne jeden gedanklichen Trick. Es ist gegeben und verborgen in der natürlichen Ordnung der Zahlen. Man muß es mal primitiv hinschreiben - wenn man darüber sprechen will.
Zurück zu: Konzentrat: "Relative Häufigkeit von Primzahlabständen"
Sie lasen bei den 'kleinen Primzahlen' - mit einem Link zu dem kostenlosen Super-Programm:
Primzahlen oder die Magie der Zahlen http://euroware.de von Reinhold Kiebart
