Wer kennt sie nicht, die doppelten Zwillinge 101,103 und 107,109, die einen "Vierling" liefern. Mit 97 und 113 wird daraus sogar ein "Sechsling":

97   101 103 - 107 109   113
anders geschrieben   105 ±2^1 ±2^2 ±2^3

Die 2er-Potenzen bedingen, dass die zusammengesetzte Mittenzahl 105 die Faktoren 3 und 5 haben muss. Das ist am Rande bekannt und wird einfach so hingenommen. Bis zu diesem Schritt ist auch nichts Aufregendes zu erkennen.
Doch wie sieht es aus, wenn wir die Fronten wechseln? Statt ±2^n setzen wir ±3^n und nehmen eine Mittenzahl ohne den Faktor 3, dafür aber mit den Faktoren 2 und 5.... Zum Beispiel:

1750 ±3^1 ±3^2 ±3^3 ±3^4
schön geordnet:
1669 1723 1741 1747         1753 1759 1777 1831
 -81  -27   -9   -3   1750    +3   +9  +27  +81

Tatsächlich ist dieser Primzahl-Achtling ähnlich aufgebaut, wie der Vierling (Sechsling) in der zweiten Zeile und es sind diesmal 8 Primzahlen, die aus den 3er-Potenzen resultieren. In meiner Terminologie heisst dieser Zahlenblock ein "3er-Achtling" mit der Mittenzahl 1750.
Ist das nun ein Einzelfall? Absolut nicht. Jede Primzahl kann statt der üblichen 2 als Basis angenommen werden. Dabei steigt die Häufigkeit solcher "Primzahl-Mehrlinge" mit größeren Basen sogar an. Aber auch zusammengesetzte Zahlen können als Basis dienen. Sehen wir uns dazu einen "Zehnling" an, mit der Basis 22 (=2*11). Wieder werden je 5 Potenzen subtrahiert/addiert und je 10 Primzahlen gefunden, die richtige Mittenzahl vorausgesetzt:

-22^5 -22^4 -22^3 -22^2 -22^1   50791275   +22^1 +22^2 +22^3 +22^4 +22^5

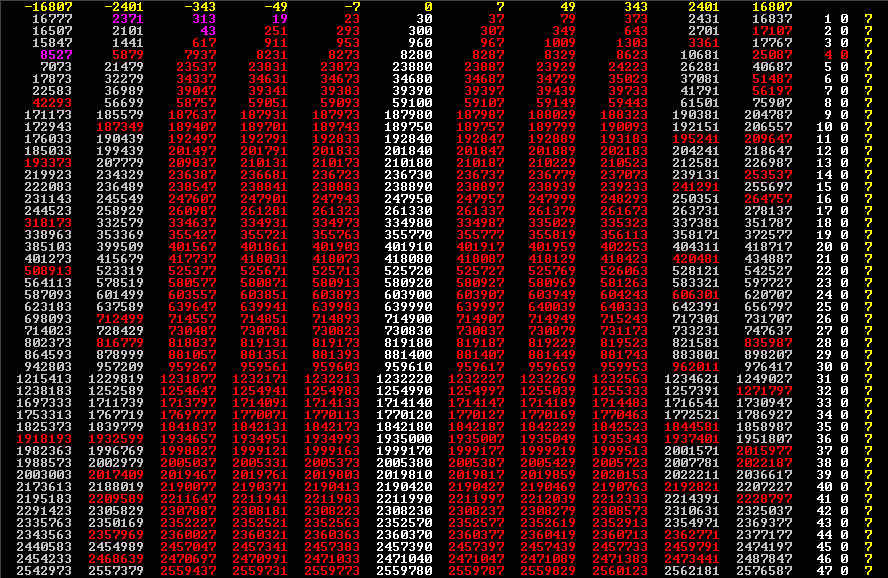
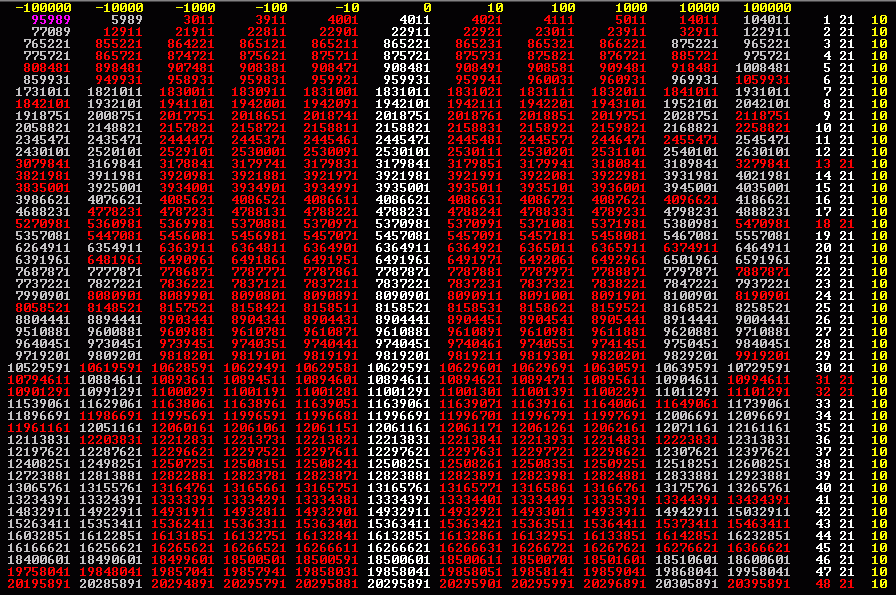
Dick angemerkt sei: Trotz relativ vieler "Primzahl-Mehrlinge" mit Basen >2, bleiben Zehnlinge dieser Art doch seltene Vögel. Die 2 folgenden Bilder zeigen einen Ausschnitt der Programm-Resultate für Potenzen von 7 und 10. Man beachte die Abstände von Sechsling zu Sechsling. Aber auch die verstreuten Achtlinge oder einen "beinahe" Primzahl-Zehnling! Primzahlen sind ROT (oder LILA), andere Zahlen sind teilbar.

Desillusion

Es liegt mir sehr daran, nicht den Eindruck zu erwecken, es sei der Stein der Weisen gefunden! Alle bisher gezeigten Zusammenhänge sind nicht mehr, als ein Blick auf die zufällige Primzahlverteilung. Es lässt sich leicht zeigen, dass jede beliebige Kombination von Potenzen ebenfalls "Primzahl-Mehrlinge" liefert.... Der folgende "gemischte" Zehnling - wieder einer von vielen - hat links Potenzen von 19 und rechts Potenzen von 17 und liefert dennoch 10 saubere Primzahlen:

-19^5 -19^4 -19^3 -19^2 -19^1   83916000   +17^1 +17^2 +17^3 +17^4 +17^5

Es ist kein erbauender Satz der Zahlentheorie damit verknüpft. Aber es ist schön anzuschauen, das Spiel mit der Aufsummierung von Potenzen! Klicken Sie mal auf meine Vermutungen .... Dort sollte deutlich werden, dass in der unendlichen Zahlenmenge Primzahlabstände in beinahe jeder denkbaren Kombination anzutreffen sind. So auch jene anderen "Mehrlinge" - abseits der gewohnten Vierlinge!