Zahlentheorie, nicht nur für die Unterstufe


Es gibt keinen einfachen Beweis unendlich vieler Primzahlzwillinge! Aber, ein guter Schüler verfügt heute über ein Basiswissen, mit dem er die Existenz von Primzahlzwillingen an jedem Ort der Zahlengeraden beschreiben und verstehen kann. Dazu zwei Axiome der Mathematik:
 1. Frage:  Wie häufig sind Primzahlzwillinge ?
---------------------------------------------------
Einige vereinfachte Bezeichnungen:
x       Schranke, ein beliebiger, hoher Punkt auf der Zahlengeraden
pi      Anzahl der Primzahlen unterhalb x
v       Intervall, ein Zahlenbereich beginnend oder nahe bei x
pi2    Anzahl der Primzahlzwillinge in v
s       10er Exponent für Stellenzahl der Schranke x
ln      natürlicher Logarithmus
lg       dekadischer oder 10er Logarithmus
C"     Konstante, die die Umrechnung von ln in lg einschließt
        C" enthält auch die sogenannte Zwillingskonstante.      
        Mit sehr hoher Näherung ist   1/C" = 4   (genauer = 4.0156...)

Zu jeder Schranke x=10^(10^s), das sind 10^s Dezimalstellen, kann das notwendige
Intervall  für jede gewünschte Menge pi2 von Primzahlzwillingen angegeben werden,  
        v = (1/C") * pi2 * (lg x)^2   oder                           
noch einfacher, da  lg x = 10^s   und   (lg x)^2=10^2*s  ist ...
    v = 4 * pi2 * 10^(2*s)
Ein Beispiel: Die größte bekannte Primzahl lag längere Zeit nahe bei
7 Millionen Dezimalstellen,  also bei s=7   und   x = 10^(10^7 ) .  
Für diese Schranke und gewünschte 250 Primzahlzwillinge
ergibt sich in sehr guter Näherung ein konkretes Intervall v
        v = 4 * 250 * 10^14 = 10^(14+3) = 10^17     | knapper geht es nicht |
Für 10^s kann jede Stellenzahl - auch gegen abzählbar unendlich - angenommen werden.

1. Antwort zur 1. Frage:  
Für jede Stellenzahl kann ein Intervall v mit einer gewünschten Anzahl von Zwillingen berechnet werden.

Und... wenn Primzahlzwillinge in beliebiger Menge gegen unendlich vorhanden und berechenbar sind, dann gibt es dort auch jenen einen gesuchten Primzahlzwilling.

 Damit ist der Schritt gegen unendlich beschrieben. Das Wort Beweis wurde sorgfältig vermieden.

2. Frage:  Wie häufig sind Zwillinge gegenüber anderen Primzahlabständen ?
---------------------------------------------------------------------------------------
Vorab, ohne jede Vermutung: Es ist ein festes Gesetz des gesamten Zahlenraumes!
In jedem beliebigen, hinreichnd großen Intervall gilt für die existierenden Primzahlabstände:
Die Abstände 2 (Zwill.), 4, 8, 16 usw. sind alle etwa gleich häufig, sie haben nur den Primfaktor 2.
Die Abstände 6,12,18,24,36,48,54 usw... alle etwa doppelt so häufig, ... da nur Primfaktoren (2) 3 im Spiele sind.
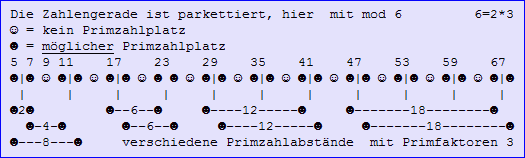
Grafik mod 6

Überzeugen Sie sich selbst:  Gezählt werden Abstände beginnend in einem Intervall (hier v=6) nach rechts. 
Wählt man eine Parkettierung mit anderen Primfaktoren, können Mengen-Aussagen zu jenen anderen Abständen gemacht werden. Daß es sich hier um mögliche Primzahlplätze handelt, spielt keine Rolle. Denn beim Streichen der Primzahlen nach Eratosthenes werden in großer Zahl und guter Verteilung alle Plätze und Abstände betroffen. Voraussetzung: Hinreichend große Intervalle, nur dann erhält man eine gesicherte Statistik !!

Einfache ergänzende Überlegung:
Nehmen wir die mit Ziffern versehene Zeile des obigen Bildes. Sie zeigt die Zahlenfolge nach dem Streichen der Vielfachen der Primfaktoren 2 und 3. Nun streichen wir eine weitere, beliebige Primzahl. Was passiert? 
  • Jede beliebige Primzahl hat nur einmal den Abstand 2 zu einer anderen Primzahl,
    aber sie hat genau zweimal     den Abstand 6 zu einer anderen Primzahl.
    6er Abstände entfallen somit doppelt so oft als Primzahlzwillinge, denn sie sind eben doppelt so häufig vorhanden.
    •
Diese exakte Zählweise beim Streichen von Primzahlen ist ohne Einschränkung gültig, auch bei jedem Eratosthenes-Streichen von Vielfachen größerer Primfaktoren. Das sollte man voll erkennen.

2. Antwort zur 1. Frage:  
Wenn nun von jedem geraden Primzahlabstand eine beliebige Menge an jedem Ort des gesamten Zahlenraumes vorhanden ist, dann gibt es als Folge auch jenen einen Primzahlzwilling - gegen unendlich.

3. Antwort zur 1. Frage:
Gelegentlich wird - selbst von hochkarätigen Mathematikern - angezweifelt, ob es in höchsten Bereichen überhaupt noch zur Bildung von Primzahlzwillingen kommen kann. Als Grund wird ausgeführt:
    "... Der Abstand zwischen Primzahlen kann beliebig groß werden..."
Das ist vollkommen korrekt, allerdings mit einer falschen Schlußfolgerung. Denn ganz im Gegenteil: In jenen hohen Bereichen sind selbst die mittleren Primzahlabstände schon extrem groß. Und nur durch das Auftreten von 'beliebig großen Abständen existieren an anderen/benachbarten Orten in konsequenter Weise 'beliebige' Verdichtungen. Die höchste Verdichtung ist dann ein nicht gestrichener Primzahlzwilling - oder auch mehrere dieser interessanten Gesellen!

 Mehr zu diesem Thema unter:   Konzentrat:  "Relative Häufigkeit von Primzahlabständen"