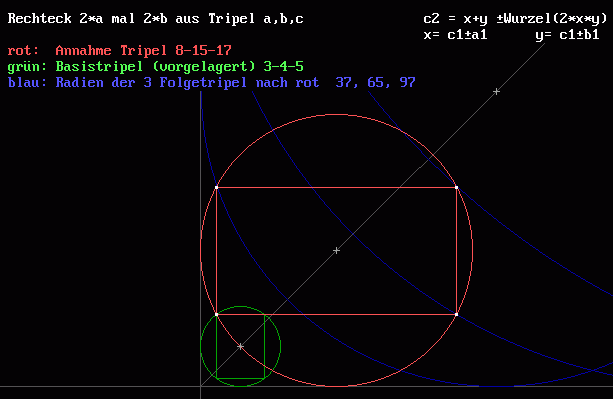
4 Rechteckpunkte bestimmen 4 Nachbartripel
|
Grafik zu Folgen von Zahlentripeln |
Spaß an Zahlen möchte ich vermitteln, möglichts ohne Formeln. An einer quadratischen
Gleichung komme ich bei den pythagoreischen Tripel (PT) jedoch nicht vorbei. Die Lösung
dieser Gleichung lautet:
|
c2 = x + y ± Wurzel ( 2*x*y ) |
|
mit x = c1 ± a1 und y = c1 ± b1 |
Durch diese Abhängigkeit einer zweiten Hypotenuse c2 von einem beliebigen ersten Tripel a1_b1_c1 kann die unendliche Welt der Zahlentripel rekursiv beschrieben werden! Letztlich läuft alles auf die Folgen A S D hinaus, wie unter Trimzahlen beschrieben. Ich suchte jedoch nach einer Beziehung, die alle Fälle benachbarter Tripel direkt abdeckt. Auch sollte dabei erkennbar werden, daß die Anzahl der Folgetripel nicht zufälligerweise 3 ist, sondern mathematisch/geometrisch begründet werden kann.
Hierzu ein simpler Arbeitsvorschlag:
Wählen Sie ein beliebiges Tripel a_b_c und ziehen Sie im ersten Quadranten eines Koordinatensystems
einen Kreis mit einem Radius c (Hypotenuse von a_b_c) so, daß der Kreis die Achsen X
und Y tangiert. Ordnen Sie in dem Kreis ein Rechteck an, das die Seiten 2a und 2b besitzt.
Das Rechteck kann horizontal oder vertikal liegen. Seine 4 Eckpunkte auf dem Kreis haben jeweils
ganzzahlige Koordinaten x und y. Durch diese 4 Eckpunkte lassen sich 4 neue Kreise ziehen,
die wieder die Achsen X und Y tangieren. 4 Nachbartripel zu dem beliebig gewählten
Tripel sind gefunden, ein kleineres Ausgangstripel und drei größere Folgetripel!

4 Rechteckpunkte bestimmen 4 Nachbartripel
Da die Vorzeichenwahl eventuell Kopfzerbrechen macht, hier ein Programmausschnitt. Dabei wäre zu beachten, daß während der Berechnung a<b zu wählen ist. Dagegen für die Ausgabe möglichst... a= ungerade, b=gerade
D: x=c-a y=c+b c=x+y+sqr(2*x*y) a=c-y
b=c-x
S: x=c+a y=c+b c=x+y+sqr(2*x*y) a=c-x
b=c-y
A: x=c+a y=c-b c=x+y+sqr(2*x*y) a=c-x
b=c-y
___ und für das vorgelagerte Tripel gilt immer:
x=c-a y=c-b c=x+y-sqr(2*x*y) a=abs(c-x) b=abs(c-y)
Ergebnis:
Tripelfolgen dieser Art lassen sich auch grafisch ganz nett darstellen. Letztlich sind es Konstruktionen,
die man früher nur mit "Zirkel und Lineal" angefertigt hätte. Heute geht
es etwas rascher und sieht dann so aus:
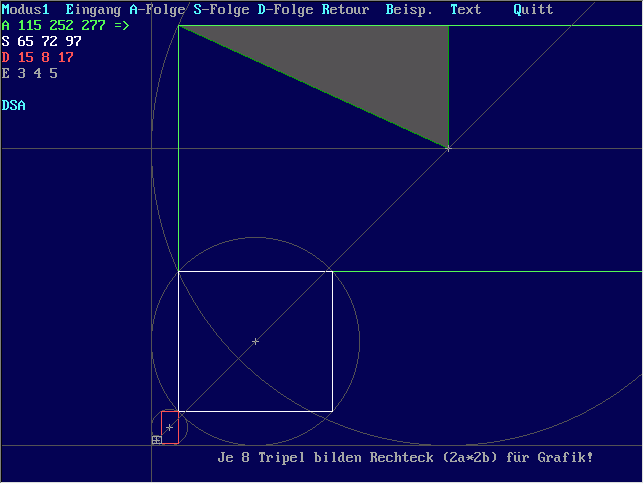
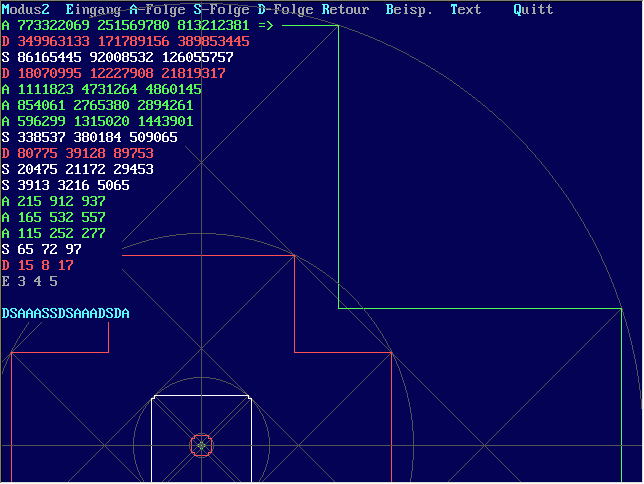
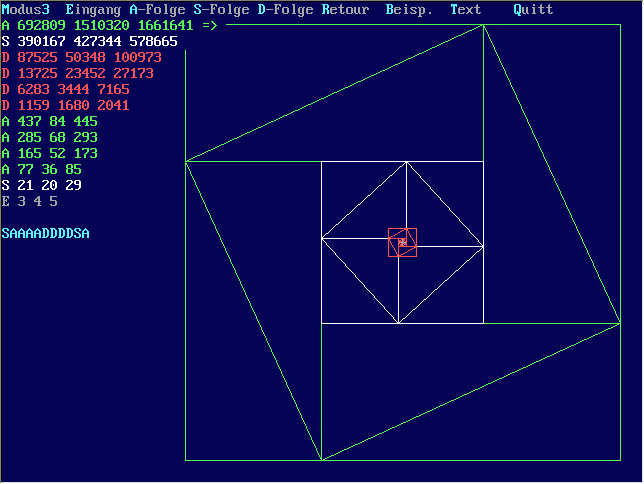
Download:
Was sollen alle meine Bemühungen? Wenn Ihr Rechner noch heil geblieben ist und ein DOS-Programm
starten kann, dann laden Sie sich trip-asd.zip auf Ihre Platte
(38.9 KB). Das fast selbsterklärende Grafik-Programm trip-asd.exe rechnet und demonstriert
Folgetripel in 4 (5) verschiedenen Darstellungen.
Viel Spaß wünsche ich beim Tripeltippen, keine harte Arbeit, ... eventuell eine Mail an mich.
|
Unlösbare (?) Aufgabe:
.... ähnelt der Einbahnstraße des ULAM-Problems |