Das Ziel dieser Homepage ist, rund um "prim" bestimmte Zusammenhänge aufzuzeigen, möglichst ohne abgeschriebene Formeln, aus eigener Sicht. Zu meiner Adresse "primini" passt hervorragend, selbstmörderisch über die kleinste Primzahl nachzudenken. Ich fand zu meinem Lieblingsthema eine Adresse - leider ohne den Autor - sinngemäss mit folgendem Titel:

Warum ist die 1 keine Primzahl ?  
http://www.lrz.de/~hr/tmp/prim.html
oder   http://www.lrz-muenchen.de/~hr/tmp/prim.html   (Geben Sie das bitte so im Browser ein.)

Schalten Sie hin. Der Autor versucht sich an dem Thema und .... Sie werden nachher kaum schlauer sein, als Sie es vorher waren. Auch bilde ich mir nicht ein, ICH könne die 1 zur Primzahl erheben und sage vorab ganz klar: 

Die von klugen Köpfen getroffene Definition der EINS muß stehen bleiben. 

Gleichzeitig füge ich an: Ein Mathematiker mit sehr gutem Namen sagte mir, er könnte auch mit der 1 als Primzahl leben, wenn es denn wichtige Gründe gäbe. Ich meine, Gründe gibt es, zumindest mal selbst darüber nachzudenken. Auch dann, wenn es unter dem 'Niveau' der meisten Mathematiker liegt.

Primzahlverdichtung, Primzahlzwillinge, Zahlengerade von - bis + unendlich, Zahlenstrahl

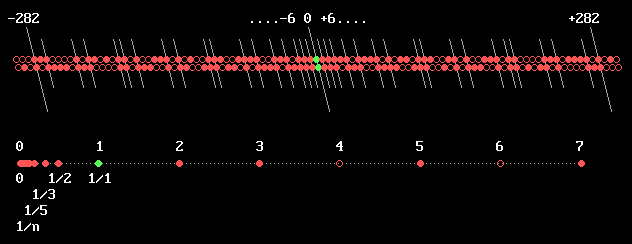
Dazu die folgende Grafik... Obere Zeile:
Es ist eine aufbereitete Zahlengerade, hier etwa von -300 bis +300. Sie zeigt alle ungeraden Primzahlen, die 6*k ±1 entsprechen. (Die Grafik entsteht dadurch, daß man die einfache ± Zahlengerade zu einer "Wendel" mit der Steigung 6 aufwickelt und alle geraden Zahlen weglässt.)
Die schrägen Linien markieren die Primzahlzwillinge - auch jene im negativen Bereich.
Die beiden günen Punkte in der Mitte sind: oben -1 und unten +1. Zwischen den beiden steht die 0. Rechts der grünen Punkte liegen somit:

....(-1) 5 11 17 23 29 -- 41 47 53 59 -- 71 -- 83 89 -- 101 107 ....
.....(+1) 7 13 19 -- 31 37 43 -- -- 61 67 73 79 -- 91 97 103 109 ....

Es ist deutlich zu erkennen: Die natürliche Verdichtung der Primzahlen und der Primzahlzwillinge um den Nullpunkt! Lediglich die "nichtprime" -1 und +1 stören und sollten als "prime" Einheit und - wenn Sie erlauben - als "Einheits-Zwillinge" (...Primzahlzwillinge) an der ±Grenze erkannt werden. Dann wird es freundlicher in der Stube!  

... für die untere Zeile:
Sie zeigt den positiven Zahlenstrahl im Bereich von 0 bis 7, also die Primzahlen 2, 3, 5 und 7. Sie zeigt aber auch die Orte der Reziprokwerte aller Primzahlen in unendlicher Dichte bis zu der unerreichten Null.
Die Verdichtung der Primzahlen und ihrer Kehrwerte wird wieder durch die grüne 1 unterbrochen, wenn wir die Einheit 1 als "nichtprim" sehen. 1/1 ist nun mal 1 und steht logisch an dem gegebenen, primen Platz dieser Zahlenfolge.

1 ist immer einer der Reste bei einer Vorauswahl modulo m      Was heisst das?

Am einfachsten erkennt man es so:
Jede ungerade Zahl (also jede Zahl die mod 2 den Rest 1 ergibt) ist primverdächtig. Sie ist nicht prim, wenn sie durch eine Zahl >2 teilbar ist.
Oder mit anderen Produkten:
Jede Zahl, die mod 6 (=2*3) einen der Reste 1 oder 5 ergibt, ist primverdächtig. Sie ist nicht prim, wenn sie durch eine Zahl >6 teilbar ist.
Jede Zahl, die mod 10 (=2*5) einen der Reste 1,3,7 oder 9 ergibt, ist primverdächtig....
Jede Zahl, die mod 30 (=2*3*5) einen der Rest 1,7,11,13,17,19,23 oder 29 ergibt, ist primverdächtig....

Immer ist der Rest 1 im Spiele und immer dann ist eine Zahl prim, wenn sie nicht durch eine teilende Primzahl teilbar ist.    Was heisst teilend?

"Teilende Primzahlen" - im Unterschied zu der 1 - wären meine gedankliche Brücke, also alle heute geltenden Primzahlen von 2 bis unendlich. Würde man diesen Zusatz in zig-zig-tausend vorhandenen Schriften machen, stünde meiner primen 1 nichts im Wege. Und Goldbachs Vermutung wäre geradezu simpel, sie lautet

Schließlich noch ein Querverweis, wieder passend zur heutigen Definition der EINS,
Primzahlzwillinge: Die Einheit aller Primzahlabstände, daraus ist entnommen:

Das Ende vom Lied ist diesmal nicht "QUOD ERAT DEMONSTRANDUM", sondern: Es muß und wird alles beim Alten bleiben... wie nun mal definiert und millionenfach geschrieben. Aber ICH sehe die EINS nicht als das ausgeschlossene Stiefkind, sondern als meine viel geliebte "prime Einheit 1". Sie auch? Und erinnern Sie sich bitte immer an meinen Primzahlzwilling bei null - pardon - meinen primen Zwilling " -1 und +1" !