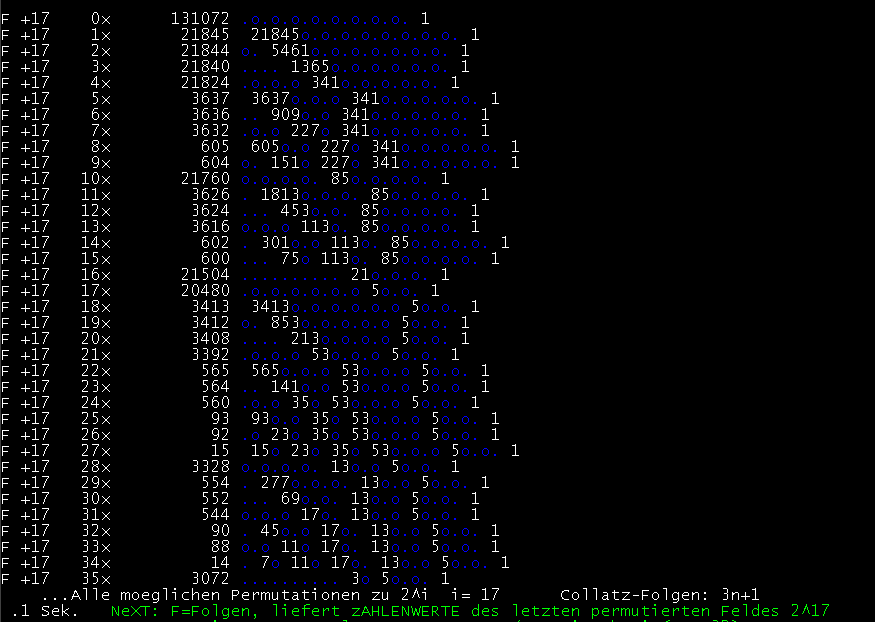
Bild zu "F"
Demo:
Permutation von Collatz-Folgen 2^i
Die Permutation von Collatz-Folgen stellte ich 2010/11 mit dieser Homepage ins Netz. Ich erwartete eine Flut von Mails, was leider ausblieb. Die einzige Zuschrift kam in 2015 von einem jüngeren Dr. der Mathematik, der meine Ergebnisse aufnahm, wenn sie denn stimmen sollten. Er prüfte es eingehend und erarbeitete einen Beitrag, den er bei einen beduteten dutschen Verlag einreichte. Leider erhielt er eine Absage. Man sei gezwungen zu selektieren, da zu viele Einsendungen vcorlägen... Was ist da zu tun?
Ich bin von der vorgestellten Lösung des Collatz-Problems überzeugt und fasse nochmals zusammen:
• Jede Collatz-Folge ist
direkt rückfführbar auf eine Basisfolge 2^i. Nimmt man
2^i als
Startwert für Collatz an, dann wird exakt nach i Divisionen die
angeblich 'unbewiesene' EINS erreicht. Das ist die Basis! Nun kann der
Verlauf der i Divisionen verändert werden, ohne das wichtugse und
konstante Ende mit ...16,8,4,2,1 zu
tangieren.
Für eine Permutation sind die zwei Collatz-Gleichungen gegeben...
n' = n/2 und n' = 3*n+1 dazu die Collatz-Basisfolge 2^i
Permutieren ist das gezielte Vertauschen einer Collatz-Division gegen eine Collatz-Multiplikation.
Jeder zweite Potenzwert der Collatz-Folge 2^i liefert mod 3 den Rest 1.
Genau vor diesen Stellen wird eine ungerade Zahl n=(n'-1)/3 statt der vorhandenen Division eingesetzt.
Damit ist die Permutation
an diesem Punkt durchgeführt. Nur der Startwert der neuen,
geänderten Fplge
ist
noch zu ermitteln.
Die existierenden Divisionen (links von n)
werden als
Multiplikation für n mit 2 abgearbeitet.
Mit anderen Worten:
n wird von rechts nach links entsprechend der ansteigenden 2er-Potenzen mit 2 multipliziert.
Bilder der alten und neue Folge:
alte Folge
2^7= 128 / / /
/ / / 1
128 64 32 16 8 4 2 1 zu pemutierende Folge mit dem Ende EINS
Das gleiche Prozedere wie für
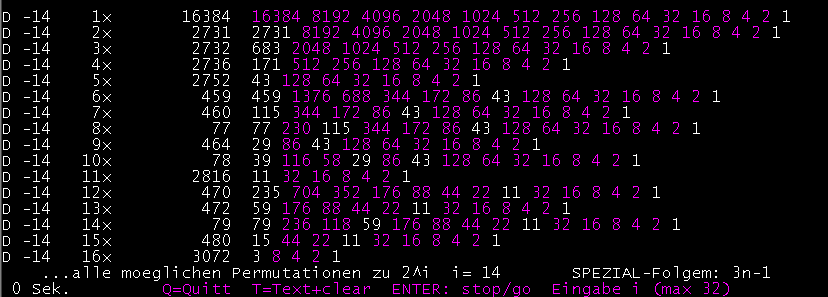
Collatz 3n+1 ist auch verwendbar für Folgen 3n-1. Im Programm wird mit
der Taste 'M' (+Enter) die Situation 'Minus' vorgewählt. Es kann hierbei
Keine
Schleifenbildung entstehen, denn die perfekte Ausgangsfolge 2^i ist immer schleifenlos!!
Die Anzahl möglicher
Permutationen bei 3n-1 ist etwa 10% niedriger als bei Collatz mit 3n+1.
Diese 10% sind jeme Startzahlen die bei 3n-1 zu Schleifen führen:
Erste Veröffentlichung 2010/11 - neueste Version vom
Ende 2016. Es lohnt sich !
Das
Programm zeigt alle
möglichen Permutationen von Folgen mit bis zu i=32 Gliedern.
Es sind alle möglichen Collatz-Folgen, basierend auf 2^i. Diese Darstellung soll keine Mathematik ersetzen. Aber ich möchte Ihnen die sehr
informative Aufbereitung nicht vorenthalten. Allerdings, ohne Programm - nur mit
Bleistift und Papier - stößt man schnell an seine Grenzen...
Höhere Startwerte als 2^32 machen für die Demonstration der Permutation
wenig Sinn. Die Laufzeiten sind zu lang und es wird unübersichtlich, obwohl alles gültig
ist bis abzählbar unendlich.
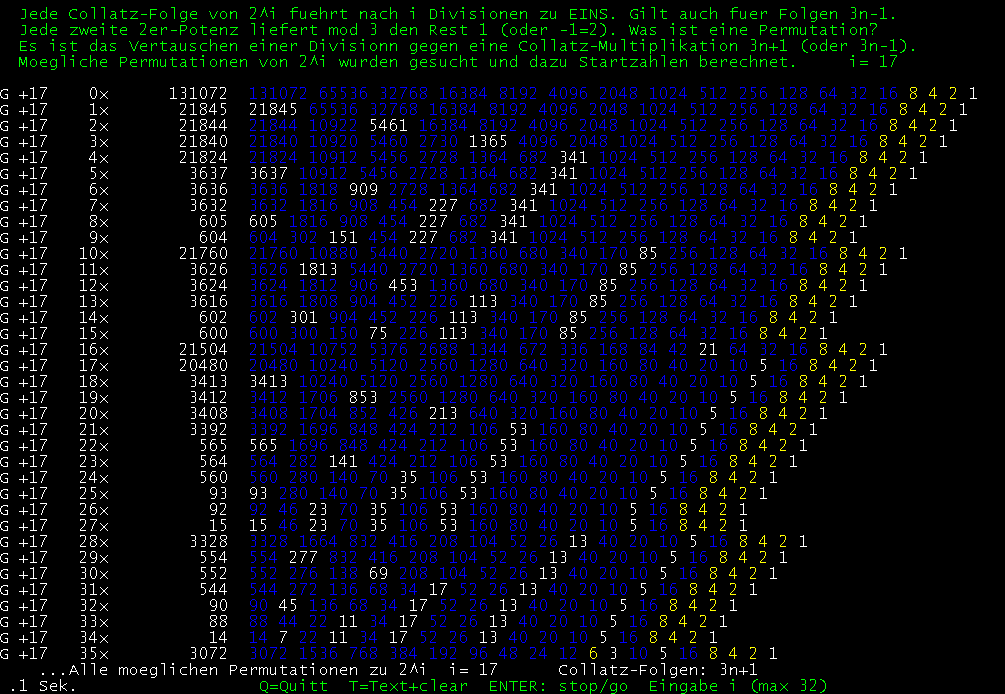
Bedienung des Programms, etwa für i=2^17:
Nach Eingabe von 17 (+ENTER) erhält man alle 35 möglichen Permutationen für 2^17.
Für i=32
sind es schon 1173 permuttierte Zeilen...
(G +Enter ... voll ausgeschriebene Zahlen der Collatz-Folgen)
(D +Enter ... gleiche Folgen, jrdoch beginnend mit erster ungerader Collatz-Zahl)
F + Enter ... Kurzform, ungerade Collatz-Werte
(Alle 35 möglichen Collatz-Folgen durch Permutation von 2^17 )
Bild zu "F"

Bild "G"