Eine geschlossene Springertour nennt man den korrekten Weg eines Springers über das Schachbrett, wenn dabei alle Felder nur einmal besetzt werden und mit dem letzten Zug wieder das Ausgangsfeld erreicht wird. Es gibt eine unübersehbare Menge von Lösungen. Ungeachtet dessen, ist es gar nicht so einfach eine eigene zu finden. Symmetrische Wege des Springers sind selten anzutreffen, da diese einen weiteren Schwierigkeitsgrad bedeutet. Beinahe zu erwarten ist, daß

eine solche Lösung angibt. Er ging ökonomisch vor und suchte 31 Züge in der oberen Hälfte des Brettes, drehte diese exakt in die untere Hälfte und wählte eine geeignete Verbindung durch 2 Züge. Fertig!
Von Euler lernen ist immer gut. Ich wählte 16 Züge als Basis, beliebig am ganzen Brett verteilt und drehte diese 3x in Schritten von jeweils 90°. Man könnte sagen, es ergeben sich auf diese Weise 4 Hamiltonsche Kreise. Findet man dann die richtigen Kopplungen, entstehen interessante Symmetrien und hunderte von Lösungen für geschlossene Springertouren. Doch wo bleiben die angekündigten

Wenn Sie diese Homepage etwas genauer ansehen, dann finden Sie an mehreren Stellen eine mögliche Eigenschaft ungerader Mengen von Primzahlen. Die Dreiersummen haben es mir besonders angetan. Mit Kenntnis dieses "primen Musters" können Sie den richtigen, symmetrischen Weg des Springers im rechten Bild finden. -  Das Schachbrett wurde durch Gitterpunkte ersetzt, um die Grafik besser zu zeigen. Tip: 8 Züge sind direkt vorgegeben!

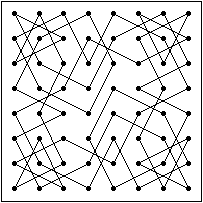
Linkes Bild:   Eine symmetrische 64er Springertour
Rechtes Bild: Eine andere, ähnliche Tour mit 64 Primzahlen als "Pathfinder"
Es wurden die ersten 64 ungeraden Primzahlen 3 bis 313 verwendet.
Falls keine Primzahltabelle zur Hand, es sind die folgenden Primzahlen im Spiel:
101, 163, 191, 193, 199, 223, 239, 241, 263, 271, 293, 313, 337, 349, 373
379, 383, 389, 401, 421, 439, 443, 457, 461, 463, 491, 503, 521, 547, 557
563, 571, 577, 587, 593, 601, 619, 641, 643, 653, 659, 673, 677