Es gibt eine unübersehbare Menge besonderer Primzahlen. Damit meine ich nicht die Klassiker der Zahlentheorie. Nein, hier geht es um absolut zufällige Eigenheiten, auf die man stößt, wenn man sich mit Zahlen beschäftigt.

Spezielle Primzahl-Palindrome
Das sind Primzahlen, die vorwärts und rückwärts gelesen eine gleiche Ziffernfolge haben.. In dem Zahlenbereich bis deutlich über 100 Stellen finden sich nur die 4 folgenden Primzahlen mit der Zahlenfolge 373... Wobei die letzten 3 Zahlen mit höchster Wahrscheinlichkeit Primzahlen sind.....  Sie sind auch perrin-prim.

Für andere Zahlen dieser Art ergibt sich kein so elegantes Bild. So sind etwa für die Folge 151... folgende Stellenzahlen prim: 3, 15, 49, 63, 89...
797.... ist prim und dann erst wieder ein Palindrom mit 357 Stellen.  797979797......

" Links- und rechtsbündige " Primzahlen
Diese erklären sich beinahe selbst. Die beiden 15- und 10-stelligen Primzahlen 724933839979337 und 1979339339 sind die größten ihrer Art. Streicht man eine Ranziffer erhält man eine neue Zahl. Sie ist prim, bzw. nicht teilbar:

.... Purer Zufall, schön anzusehen, von Interesse für manche Menschen und ohne jeden Nährwerte für viele!

Primzahldreh  (ohne Worte)

Fortsetzung folgt....
 

Es wird zwei Arten von Lesern meiner Seiten geben. Die einen haben einen direkten Bezug zu Primzahlen. Die anderen fragen: "Was soll ich damit anfangen?" Letzteren kann geholfen werden. Vielleicht freuen sie sich dann mit mir über ein simples Primzahldreieck, in dem aber doch einiges steckt. Das unten gezeigte Dreieck hat 11 Zahlen pro Dreiecks-Seite. Insgesamt haben 66 Primzahlen auf den Schnittpunkten der roten Linien Platz. Zum Beispiel die Primzahlen 13 bis 353in laufender Folge . Versuchen Sie mal diese Zahlen (oder andere ungerade Primzahlen in laufender Folge) in einer anderen Verteilung auf die Ecken der kleinen Dreiecke zu setzen. Für jedes kleine Dreieck gilt: Die Summe der 3 Primzahlen ist wieder prim! Es sind 100 Summen zu finden, 100 Bedingungen müssen erfüllt sein.

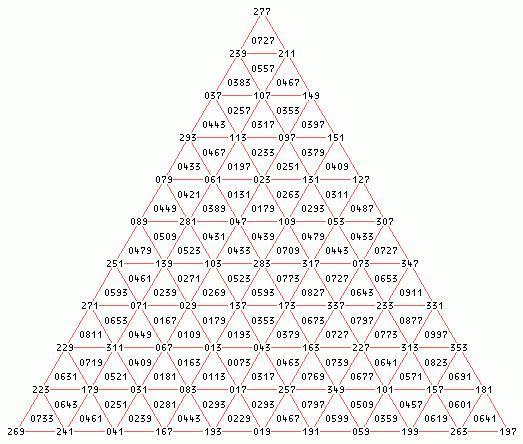
Anmerkung: Mit den 6 Primzahlen 3,5,7,11,13,17 und einem Basisdreieck bestehend aus  4 kleinen Dreiecken geht es etwas leichter - ohne Rechner! Steigert man die Schwierigkeit und nimmt jeweils eine weitere Reihe von Dreiecken hinzu, dann hat man 9, 25, 36, 49, 64, 81 und schließlich 100 prime Summen - hoffentlich!