Es ist hoch ansteckend! Ich infizierte mich im Dezember 2005 und im
Januar 2006 heilte ich es aus!
Sudoku Rätsel sind überall zu
finden, an jedem
Kiosk kann man sie kaufen. Mit Primzahlen haben sie nichts zu tun. Der
Mensch hat zwei Kontaktebenen zu dieser
Erscheinung. Einmal ist es der direkte Wunsch das angebotene
Rätsel zu lösen. Parallel dazu fordert es den
heutigen Löser - oder User - geradezu heraus,
seinen PC einzusetzen. Überrascht stellt
man fest, daß es zwar jede Menge von Versuchen gibt,
dieses Rätsel auch per Programm zu lösen.
Aber, es
existiert wohl keine geschlossene Lösung, die jedes Sudoku -
auch
ein schweres - sofort knacken kann. Das ist gut so, nutzen wir
auch künftig unseren Kopf.
Fragen
Gibt es doch eine glatte Lösung? Und wie kann
man kontrollieren, was uns da an
Aufgaben vorgesetzt wird? Gibt es bei einer gestellten Aufgabe wirklich
nur die eine Antwort, die ein 'echtes' Sudoku haben darf? Kann
man
bei einem gegebenen Rätsel den Schwierigkeitsgrad
erhöhen, in
dem man die eine oder
andere vorgegebene Ziffer einfach wegläßt? Kann man
ein Sudoku letztlich selbst erstellen und sauber prüfen? Diese
Fragen bildeten sich sehr
bald heraus, als ich in das Thema tiefer eindrang.
1. Anmerkung nach
Ausgabe des Heftes 3/2006 von 'Spektrum der Wissenschaft'
Ja, es gibt 'DIE' Lösung - für jedes
Sudoku! In der
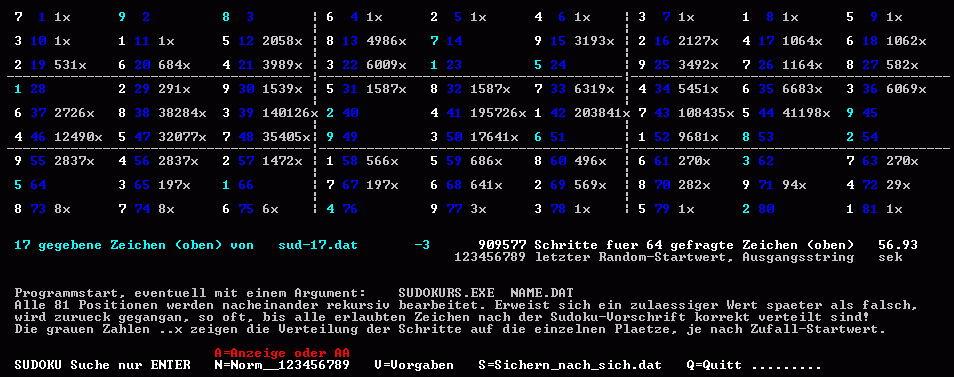
Zeitschrift wird sogar ein Sudoku mit nur 17 Vorgaben gezeigt, auch die
fertige Lösung wird angegeben. Ein anwendbares
Programm wird nicht
genannt. Daher zeige ich hier meine allgemeine
Lösung dazu - und
auch den Weg dahin.... Im nächsten Sudoku-Bild also
nur 17 Vorgaben:
2. Anmerkung im
März 2006
Inzwischen habe ich das Problemchen tiefer untersucht. Eine neue
Variante meines Sudoku-Programms liefert in der Zeit 0 (null) zu jedem
echten Sudoku ohne jede Berechnung 'beliebig' viele weitere, neue
Vorgaben...
Nicht etwa durch Spiegeln! - Bei Interesse: Mail genügt, sieht so aus:
Vorgabe
 Lösung
Lösung
Jeder Hobby-Programmierer dürfte
schnell an Grenzen
stoßen. Mir ging es nicht besser! Zum Glück
beschäftigte ich mich schon früher mit sogenannten
rekursiven Programmen. Das sind Unterprogramme die sich selbst
aufrufen.... Solche SUBs haben ihre Tücken. Sie sind aber sehr
effektiv, wenn man den richtigen Ansatz wählt. Sehr
nützlich
erwies sich hierbei der 32_Bit_Compiler von PowerBASIC PBCC.
Natürlich eignet sich dafür auch jede andere Software
mit einer guten Datenverwaltung im sogenannten Stack. Dieser
muß groß genug bemessen werden können oder
sich selbst
erweitern, eben wegen der fortgesetzten Rekursion.
Hier ist nun meine 'glatte' und schnelle Lösung für
jedes Sudoku! Werfen wir einen Blick auf
die einzige Seite des Programms, die alle Ein- und Ausgaben
enthält:
SUDOKURS.EXE
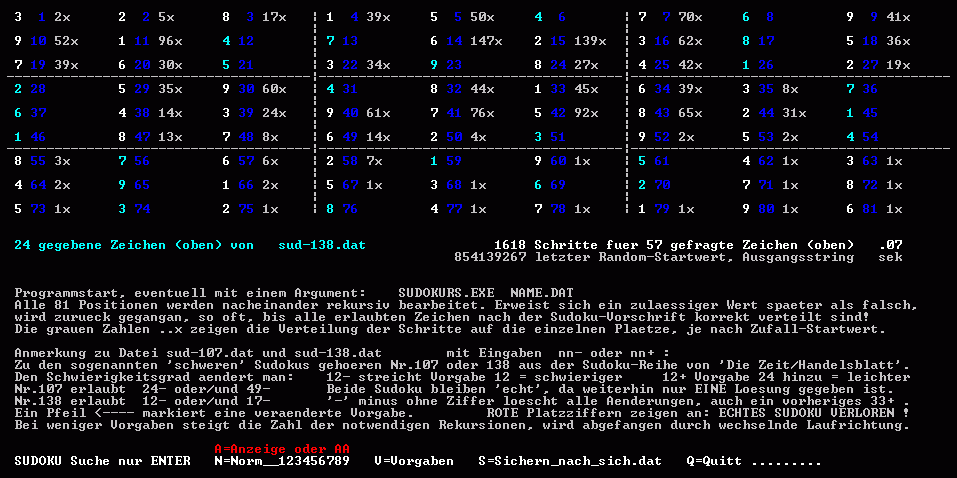
Was erkennen wir?
Oben, die weißen Zahlen sind die errechneten Werte,
türkis dagegen die 24 Vorgaben. Blau ist die laufende Nummer
des Platzes und grau die Zahl seiner rekursiven Aufrufe. Wichtiges
steht in der Mitte: 1618 Schritte (Rekursionen) für die 57
gefragten Zeichen. Alles geschah in o.07 Sekunden, wobei mein Rechner
längst nicht mehr zu den neuesten zählt!
Die weitere
Optimierung enthält: Je nach Verteilung der Vorgaben
werden
die 81 Plätze steigend oder fallend abgearbeitet,
beginnend
dort, wo mehr Vorgaben existieren. Mehrere Suchläufe
hintereinander bestätigen die Einmaligkeit
der Lösung!
Will man mehr als nur eine einfache Prüfung des
Sudoku haben,
dann
kann man Änderungen nach obigem Text versuchen! Es darf sich
dabei
an dem Ergebnis nichts ändern, außer der Zahl der
Aufrufe!
Werden jedoch ROTE Platzziffern
ausgewiesen, dann stehen diese bei einer neuen
weißen
Ziffer. Diese Ziffern sind ansich richtig - aber doch falsch,
da
sie nicht zu dem echten
Sudoku gehören, das man vor der
Änderung hatte!
Nachtrag:
A = Anzeige des Suchlaufs in optimierter Richtung, in der Regel
schneller
AA = Suchlauf in Gegenrichtung, meist langsamer,
aber auch
beeinflußt durch Startwert. In der letzten Version kann man
endlich durch jede Taste abbrechen. Dennoch gilt: Auch 300.000 Schritte
liefern korrekt das falsche Sudoku!
DOWNLOAD
Sollten Sie Interesse haben, dann holen Sie sich hier die
gezipten Daten... sudokurs.zip
20-25 kB
Nachtrag: Jene neueste obige
Variante, die beliebig viele neue Sudokus generiert... sud-107.zip
Neben den Programmen selbst sind die Eingabedateien für einige
Sudokus
enthalten.
Bitte alles in einen Ordner kopieren und starten.
QUELLTEXT zu dem einen wichtigen SUB,
daran soll es nicht fehlen, wenn jemand selbst arbeiten möchte:
n=-1 : call sudo(n+1)
SUB
sudo(n)
' REKURSIVES SUB String-orientiert
INCR
m
' m zählt Aufrufe
DO
' sucht freien Platz in Zeile/Spalte
y=n\9 : x=n MOD 9
' \ Ganzzahldivision
IF (u(y,x))="" THEN EXIT LOOP ELSE INCR
n
LOOP UNTIL n=80
' hier 0-80 oder 80-0
y=n\9 : x=n MOD 9 : z=y\3+(x\3)*3
la=LEN(fz(z)) :
i=0
' liefert direkt 1-9 Zeichen
DO
' Hauptschleife der Rekursion:
INCR i :
z$=MID$(fz(z),i,1)
' z$ AbfrageZeichen aus String
IF INSTR(fy(y),z$)
THEN
' Zeilentest von z$ und
IF INSTR(fx(x),z$)
THEN
' Spaltentest von z$
u(y,x)="+"+z$ :INCR
n(n)
' Übernahme von möglichem z$
ya$=fy(y) : fy(y)=REMOVE$(fy(y),z$) ' als "ALT"
sichern für unten und
xa$=fx(x) : fx(x)=REMOVE$(fx(x),z$) ' z$ dreimal
streichen, da verbraucht
za$=fz(z) : fz(z)=REMOVE$(fz(z),z$)
us=fy(y)+fx(x)+fz(z)
' String us="" für Ausstieg!
IF us="" OR INSTAT THEN EXIT
SUB '
erstmals notwendig !
CALL sudo(n+1) ' <----------------
RekursAufruf bis n=80
IF us="" OR INSTAT THEN EXIT
SUB '
nochmals! INSTAT: Austieg mit Taste !!
u(y,x)=""
' ...hier weiter, wenn z$ falsch war
fy(y)=ya$ : fx(x)=xa$ :
fz(z)=za$ ' zurück zu
den alten $_Strings
END IF
END IF
LOOP UNTIL
i=la
' la war die Stringlänge
END SUB
Dieser knappe Code
enthält alles! - Der Rest des Programms ist das
notwendige
Drumherum, Initialisierung, Vergleiche, Ausgabe usw.
Schlußbemerkung
Ein solches Programm soll nicht die Freude an einem Sudoku nehmen, soll
nicht Bleistift und Papier ersetzen. Es
kann aber sehr hilfreich sein, wenn man etwas prüfen oder
ändern will. Auf die Auflösung im
nächtsen Heft muß man nicht mehr warten.
Für mich war das Programmieren einer allgemein anwendbaren
Lösung mehr als
jedes Sudoku selbst!

 Lösung
Lösung
 Lösung
Lösung