|
Primzahlen - Pascalsches Dreieck - Sierpinski |
Vorbemerkung:
Ich ging bisher davon aus, daß das bekannte Sierpinski-Dreieck und das Sierpinski-Viereck (besteht
aus 9 Quadraten!) mehr an Gemeinsamkeit haben, als die Zugehörigkeit zu den selbstähnlichen
Objekten und die Besonderheit, daß bei beiden Figuren die Mitte eine "leere" Verkleinerung
der Figur aufweist. Ich nahm an, es müsse einen gemeinsamen Bauplan geben, der direkt
zum n-Eck führt. Jedoch, je intensiver man sich mit der Sache beschäftigt:
Sierpinski-Dreieck und Sierpinski-Viereck sind unabhängig und nebeneinander zu sehen!
Vor allem, das Sierpinski-9er-Viereck ist eine willkürliche Figur, die völlig anders aussehen
könnte...
symmetrisch oder unsymmetrisch, z. B.:
Original: 1 1 1 oder: 0 1 0
1 0 0 0 0
1 0 1
1 1 1 1 0 0 1 0
1 1 1
0 1 0 1 1 1
Sierpinski Dreieck
Diesem gilt hier das Hauptinteresse mit der Vorgabe: Es sollte ein dazugehöriges "echtes"
Sierpinski-Viereck (Quadrat) existieren, das zum n-Eck führt. Zwei verschiedene Prozeduren werden
zur Erzeugung des Sierpinski-Dreiecks angegeben:
Methode 1 ... nur für Dreieck geeignet!
Als Ausgang dient ein beliebiges Dreieck, vorzugsweise ein gleichseitiges. Die Punkte der Seitenmitten
werden verbunden. Es entstehen 4 kleinere, kongruente Dreiecke. Das mittlere bleibt unverändert,
die drei anderen werden wie das Ausgangsdreieck rekursiv bearbeitet...
Methode 2 ... für Dreieck angegeben, wäre prinzipiell bei allen Vielecken anwendbar!
In jedem Schritt werden von dem aktuellen Dreieck Verkleinerungen (3 komplette Kopien, linearer
Verkleinerungsfaktor k=2) erstellt und an den Ecken berührend wieder zu einem Dreieck zusammengefügt.
Beide Verfahren liefern für n=3 ein vollkommen identisches Produkt. Bei der zweiten Methode wird aber sofort erkennbar, daß das Abbild der Figur in jeder Ecke abnehmende Größe haben muß ... 1/2, 1/4, 1/8, 1/16, .... so weit, wie es unser Medium zuläßt. Man könnte im Vorgriff auch sagen: Jede Ecke ist ein Attraktor einer fraktalen Abbildung.
Pascalsches Dreieck
Ich sage mal frech: Es gibt nicht EIN Pascalsches Dreieck, aber es gibt unendlich viele! Das
kleinste P.D. mit einem Koeffizienten >1 weist in Mitte der Basiszeile die Zahl 2 aus. Vergrößert
man dieses Dreieck linear um den Faktor 2 und führt dies rekursiv weiter, erhält man unendlich
viele Pascalsche Dreiecke deren kleinste Faktoren die Werte 2, 4, 8, 16 .... haben. Alle diese
P.D. liegen zwischen 2 Strahlen, die von einer oberen Spitze ausgehen.
Markiert man im Pascalschen Dreieck alle geraden Koeffizienten, erhält man eine Darstellung
die exakt dem Sierpinski-Dreieck entspricht. Voraussetzung: Das P.D. muß mit Potenzen von 2,
also mit den Zahlen 2, 4, 8, 16, ... abschließen, genauer gesagt, eine Zeile vorher! Alle 3
Ecken haben dann ein vollkommen gleiches Muster. Oder anders ausgedrückt, jede Ecke in diesem
Dreieck - Pascal oder Sierpinski - entspricht der Spitze des Pascalschen Dreiecks.
Sierpinski-Viereck
Die obige Überlegungen zeigen, daß der Sierpinski-Viereck-9er-Teppich keine mathematische Verbindung
zu dem Sierpinski-Dreieck besitzt, außer der allgemeinen Selbstähnlichkeit. Denn beim "Teppich"
sind 9 Quadrate im Basisquadrat vorgesehen und nicht 4, wie es die Zahl der Ecken und Attraktoren
fordert.
Chaosverfahren
Es gibt ein Chaosverfahren zur Erzeugung eines Sierpinski-Dreiecks. So weit mir bekannt, wird
es erstmals (?) von Prof. Peitgen erwähnt. Das Verfahren ist eine einfache rekursive Vorschrift:
Zu einem beliebigen Ausgangspunkt wird mittels Zufallsgenerator einer der drei Eckpunkte des
Dreieckes gewählt. Der jeweils nächste, zu konstruierende Punkt liegt auf halber Strecke zwischen
dem Ausgangspunkt und dem Zufalls-Eckpunkt. Nur die gefundenen, neuen Punkte werden markiert,
keine Linien. Fertig!
Tatsächlich ist dieses Verfahren alles andere als chaotisch. Es enthält indirekt folgende Anweisung:
Jeder existierende und jeder neu entstehende Punkt wird in der Weise vervielfacht, daß auf
den 3 Strecken zwischen diesem Punkt und jedem Eckpunkt neue Punkte gesetzt werden, bei 1/2,
1/4, 1/8, 1/16 .... immer im Abstand zum Eckpunkt und immer wieder rekursiv für jeden neu gesetzten
Punkt!
Das n-Eck
Will man eine dem Sierpinski-Dreieck analoge Beziehung für n-Ecke angeben, so muß man das n-Eck
so behandeln, wie oben beim Dreieck beschrieben. Jede der n Ecken wird zum Ort für eine Verkleinerung
des n-Eckes. Der Verkleinerungsfaktor sollte so gewählt werden, daß sich die n Figuren in den
n Ecke nicht überdecken, bestenfalls tangieren. Letzteres ist insbesondere beim Viereck (Quadrat)
kritisch. Hier würden bei einer Verkleinerung um den Faktor 2 die Quadratseiten "tangieren",
was keine brauchbare Darstellung ergibt. Es muß daher geringfügig stärker verkleinert werden,
also Verkleinerungsfaktor k>2.
Günstige
Verkleinerungsfaktoren k erhält man
mit: k = 1 +
n/3
(nicht zwingend)
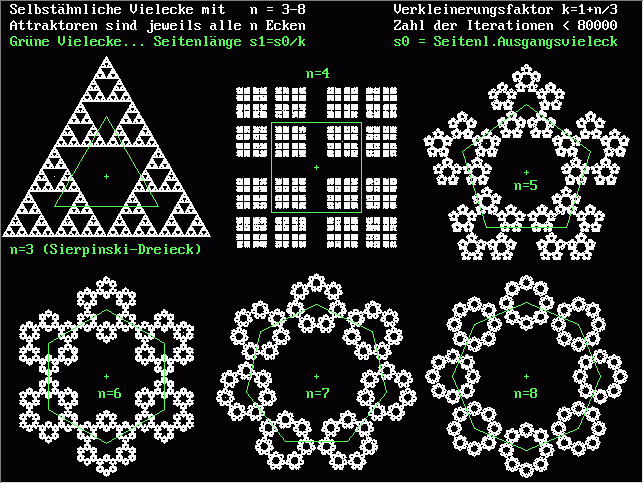
Das folgende Bild zeigt die fraktalen Figuren für die ersten 6 n-Ecke, alle mit dem gleichen Verfahren gewonnen. In Anlehnung an Sierpinskis Dreieck ist jede Ecke eines Vielecks ein Attraktor für die rekursiv verkleinerten Abbildungen desselben. Bei n=4 sind selbst in dieser pixelbeschränkten Darstellung 2^8 = 256 selbstähnliche Quadrate erkennbar.

... und zum Spaß:
Tip für die eigene Programmierung:
k~2.2 Generierung mit x:=-x und y:=-y
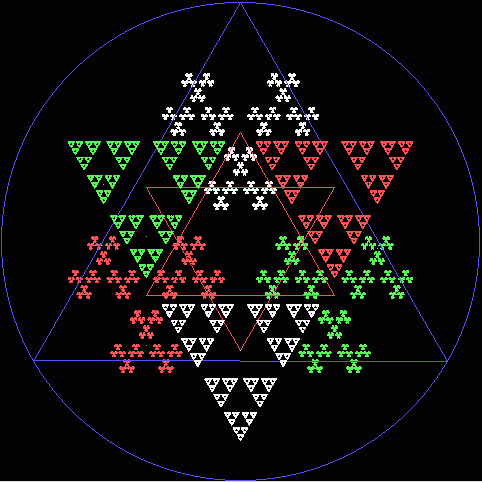
Das obere Bild liefert ein gutes Argument gegen die Aussage:
Sierpinski-Dreieck ("chaotisch" erzeugt) = Pascalsches Dreieck
Beide Dreicke ähneln sich sehr, haben eine ähnliche, sogar gleiche Geometrie. Sie sind
aber verschieden. Der Faktor k>2 genügt, die vollkommen ausgeglichene Sierpinski-Pascal-Figur
(mit k=2) zu zerstören. Im Bild sind zwischen den verschiedenfarbigen Dreiecken und innerhalb
der gleichfarbigen unzulässige Lücken. Markiert man bei Pascal die Koeffizienten für beliebige
Teiler, erhält man unendlich viele verschiedene Formen.
Jedoch, eine gestörte Harmonie, wie im oberen Bild, wird man in der Pascalschen Ordnung
vergeblich suchen.
Pascalsches Dreieck (Viereck) im dualen Zahlensystem
Genau dieses ist gegeben, wenn man im normalen P.D. gerade und ungerade Zahlen markiert. Für
die beiden Zahlen 0 und 1 gilt dann die einfache Additionsregel: 0+0=0
0+1=1 und 1+1=0
1
1 1
1 0 1
1 1 1 1
1 0 0 0 1
1 1 0 0 1 1
1 0 1 0 1 0 1
1 1 1 1 1 1 1 1
Daß dieses von Einsern begrenzte Dreieck von vornherein vollkommen identische Ecken im Hinblick auf obige Rechenregel haben muß, ist überzeugend. Interessant wird es, wenn man die gleichen Zahlen in quadratischer Form anschreibt. Wichtig ist, daß hier nun in jeder der 4 Ecken des Quadrates gleichzeitig ein Pascalsches Zählen beginnt und für jedes Viertel bis zur Mitte durchgezählt wird.
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1
1 1 0 0 1 1 0 0 0 0 1 1 0 0 1 1
1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1
1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1
1 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1
1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1
1 0 1 0 0 0 0 0 0 0 0 0 0 1 1 1
1 1 1 1 0 0 0 0 0 0 0 0 1 1 0 1
1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1
1 1 0 0 1 1 0 0 0 0 1 1 0 0 1 1
1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Programmiert man den letzten Zahlenblock, ergibt sich das linke der beiden nächsten Quadrate, Text zu rechts siehe unten.

Eingangs dieses Beitrages wird unter Sierpinski die "Methode 1" genannt. Diese könnte man für n-Ecke folgend formulieren:
Zu Bild links..."Als Ausgang dient ein beliebiges Vieleck, vorzugsweise ein regelmäßiges n-Eck. Der Mittelpunkt einer jeden Seite wird mit dem Mittelpunkt der Nachbarseite verbunden. Es entstehen n kongruente Dreiecke in den n Ecken. Im Zentrum der Figur bildet sich eine Verkleinerung des n-Ecks." (Anmerkung: ..., das wie das Ausgangs-n-Eck rekursiv weiterbearbeitet werden könnte... )
Zu Bild rechts...
Ausgangsfigur ist hier das auf der Spitze stehende Quadrat! Teilt man dieses durch die beiden
Diagonalen, erhält man 4 kongruente Dreiecke für eine Sierpinski-Füllung... Auch dieses Procedere
funktioniert ebenfalls mit jedem n-Eck und liefert rekursiv verkleinerte n-Ecke, abwechselnd
auf der Spitze stehend oder horizontal ausgerichtet!
Das obige rechte Bild erscheint mir die beste Brücke vom Sierpinski-Dreieck zu Sierpinski-n-Ecken zu sein.
In beiden Fällen wird ein so zu nennendes "Sierpinski-n-Eck" auf das klassische
Sierpinski-Dreieck zurückgeführt.
Fazit:
Es stellt sich zwingend die Frage, ob man hier nicht über das ursprüngliche Ziel hinaus geraten
ist. Denn durch solche grafischen Spielereien kann jede beliebige Figur in verschiedenster
Weise in Dreiecke aufgelöst werden. Jedes dieser Dreiecke kann dann eine Sierpinski-Tapete
aufnehmen. - Ein Beispiel an einem 5-Eck zeigt die rekursive Erzeugung von Dreiecken mit einem
Attraktor für diese Dreiecke im Zentrum und jedes Dreieck hätte in jeder Ecke wieder Attraktoren
für das Sierpinski-Muster.....
Rechts daneben finden Sie ein programmiertes Sierpinski-7-Eck. Es gehört zu dem oberen rechten
Quadrat. Beachten Sie bitte die verkleinerten 7-Ecke zum Zentrum hin....
QUOD ERAT DEMONSTRANDUM


Ihre Meinung zu meinen Überlegungen wäre eine feine Sache. Ich danke Ihnen schon heute dafür!