Zahlentripel und Primzahlen

Das Thema liegt auf der Hand, denn als primes.exe unter DOS (PowerBASIC) entstand, gab es die heutige 32bit -Welt noch nicht. Ich zögerte umzusteigen, da ich mir die bekannten Probleme der Windows-Programmierung nicht aufbürden wollte. Nun fand ich den 32bit Compiler von PowerBASIC: PBCC ! Damit kann man auch unter Windows sehr gut arbeiten und erhält kompakte Programme.

Vorab ein interessantes Ergebnis. Durch etwas Überlegung habe ich dem Zufall ein wenig nachgeholfen. Die erste Grafik zeigt eine GIF-Abbildung einer Original-Fläche von exakt 1000 mal 500 Pixel. In dem originalen Feld sind alle Primzahlen von 7 bis zu der Zahl 45.000.000 (1000x500x90=45 Millionen) exakt gespeichert. Und noch etwas steckt als Demo, und nur als Demo, in dem nächsten Bild. Die eine Hälfte ist farblich "komplementär" zur anderen. Wobei beide Ausführungen vollkommen gleichwertig sind. Wohlgemerkt, nur die Farben sind komplementär, die Primzahlen sind durchlaufend, links also andere Zahlen als rechts!

Was fällt auf bei dem Gesamtbild? Ich meine, eine bestimmte Erscheinung ist gut zu erkennen. Es laufen Strukturen von links oben nach rechts unten. Es sind keine festen Linien, aber eben Strukturen unter einer Neigung von 45°. Im linken Feld treten sie etwas mehr hervor als rechts. Nun kann man bei einer grafischen Darstellung von Primzahlen und bestimmten Vorgaben ähnliche Erscheinungen finden. Ich möchte die Frage dem Leser überlassen und die Antwort nicht angeben. Statt dessen als kleine Knobelei :

Frage 1 : Welche Bedingung führt zu der auffallenden 45°-Erscheinung?
Frage 2 : Welche Vorgabe ist zu ändern, um die Struktur um 90° zu drehen?
Frage 3 : Und in welchem Feld - links oder rechts - hat "prim" den Wert 0?

Anzumerken ist, die Antworten liegen fast auf der Hand und sind doch nicht so leicht zu finden. Sie sind zahlentheoretisch begründet, ein Grafikfehler ist nicht die Ursache der Strukturen! Auch die Art der Kodierung ist nicht Grund der Streifen. Primzahlen sind eben das würzende Salz in der zahligen Suppe. - Ich freue mich auf Ihre Mail, gleich welcher Meinung Sie sind, auch wenn Sie die Lösung nicht erkennen....

Wozu könnte man nun die "TrueColor Primzahlen" nutzen? Einzig und allein die hohe Speicherdichte ist von Vorteil. Aber aussagekräftig für das menschliche Auge sind die zig Millionen Farben nicht mehr, auch nicht gezoomt! Da lobe ich mir die 16 Farben von primes.exe !!! 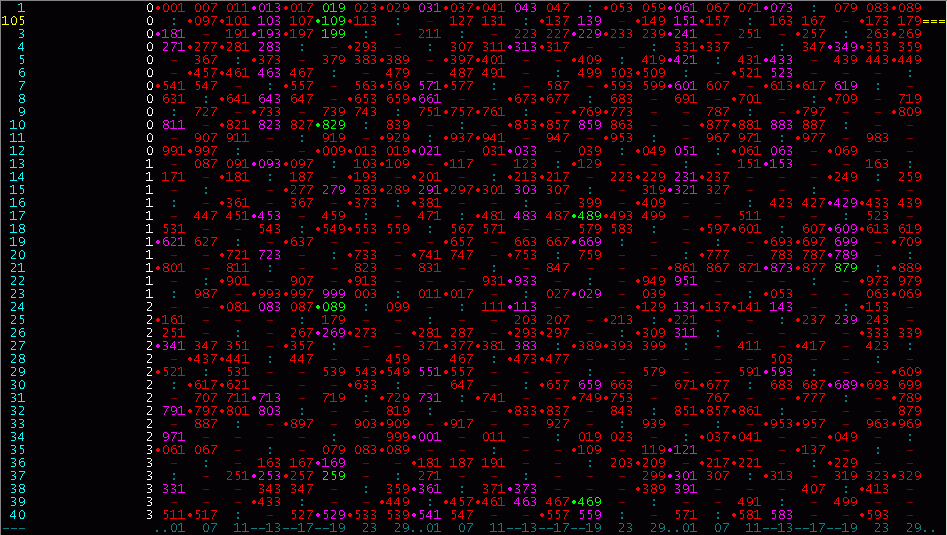Deshalb wählte ich einen anderen "pseudografischen" Weg mit dem neuen Programm primini.exe und packte die 24 primverdächtigen Zahlen eines einzigen Pixels aufgelöst in eine Textzeile. Das nächste Bild zeigt die ersten 40 Pixel der oberen Grafik als 40 Textzeilen (Seite 1). Es ist der Zahlenbereich 0 bis 3600 (=40x90). Anzumerken: Der 8-fache Zahlenbereich kann mit den 8 Seiten von PBCC geschaltet werden. Dem GIF-Bild ist eine Menge an Informationen zu entnehmen, dazu die Bildbeschreibung:
Der binäre Code von Pixel 1 (Zeile 1) ist: 000000000000010000001000 oder eben 24 komplementäre Zeichen: 111111111111101111110111 Gelesen wird - wie bei primes.exe - die weisse Zahl in Verbindung mit einer farbigen. Farbig (rot und andere) sind alle Primzahlen. Lila ist die letzte Zahl eines Zwillings und grün ist die letzte Zahl eines Primzahlvierlings. Ein Punkt vor der Zahl ist der Hinweis auf eine TRIM-Zahl, siehe dort, bei Tripel. Ein Doppelpunkt zeigt alle durch n teibaren Zahlen, voreingestellt n=7. In der 2. Zeile sieht man mit 105 die momentane Eingabe. Die letzte Zeile gibt die Reste MOD 30 aus...

40 Pixel/Zeilen

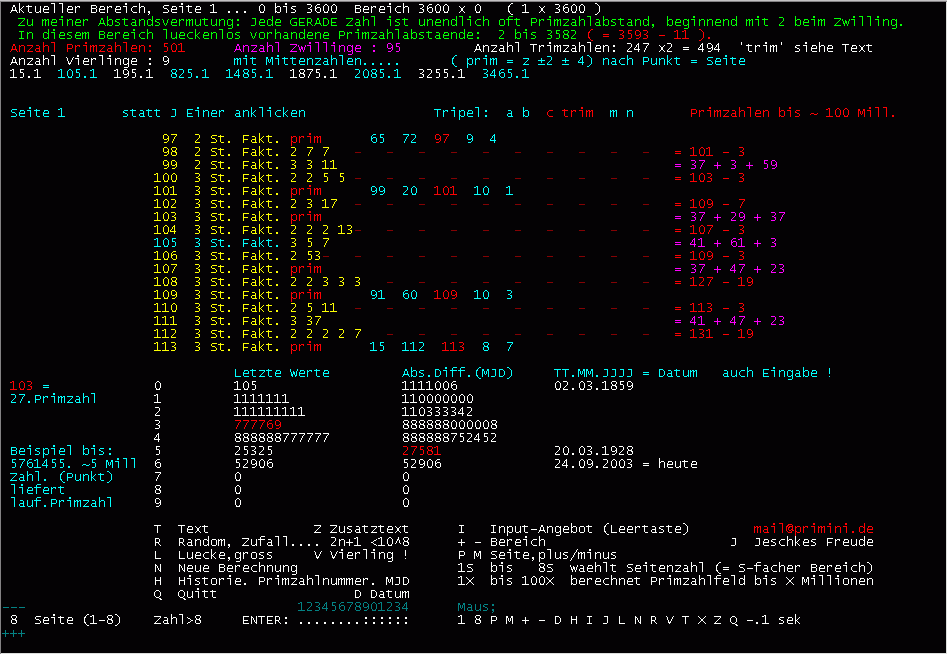
Wie erhält man die oben ausgewiesenen Werte? Nur durch Eingabe der Zahl 105, das ist alles (maximal 14 Stellen). Im unteren Bild "Seite 8" stehen eine Menge anderer Daten, die zur Umgebung der Zahl 105 gehören, wobei die ersten 6 Zeilen selbsterklärend sind.

Bildmitte: Die Umgebungszahlen des Sechslings (Mittenzahl 105) werden faktorisiert. Der zugehörige Tripel-Vierling wird ausgewiesen mit: 65^2+72^2=97^2 97=9^2+4^2 Rechte Spalte: Gerade Werte sind Differenzen von Primzahlen ... ungerade sind Summen von 3 Primzahlen. Der Zahlenblock unterhalb der Mitte zeigt die Hystorie (H), also die letzten Eingaben, die laufende Primzahl-Nummer und als besonderen Kick die Differenz der letzten beiden Eingaben, interpretiert als MJD = Modifiziertes Julianisches Datum !!! Da das Programm mit dem aktuellen Datum startet, kann durch Eingabe z.B. eines Geburtsdatums das Alter in Tagen ermittelt werden... oder eben zwei Daten eingeben mit TT.MM.JJJJ und feststellen, dass die Tagesdifferenz eventuell prim ist.

Eingabe 105

Darüber hinaus liefert mein Programm primini.exe noch eine Reihe weiterer Funktionen und Fakten, raffinierte Eingabehilfen über Einstiegszahlen usw...
Zum Beispiel "Achtlinge der Basiszahlen 2,3,5 oder 7". Noch nie gehört? Ich auch nicht, aber mit "primini" fand ich neue Pfade.
Wenn Sie sich die Sache genauer ansehen wollen, dann schicken Sie mir eine Mail. Sie erhalten das Programm natürlich kostenlos.
Einen Download möchte ich im Moment nicht anbietem, denn dann sehe ich nicht, wer damit arbeitet und erhalte wenig oder keine Antwort.

Die TrueColor-Primzahlkodierung der Überschrift wurde durch die Möglichkeiten von PBCC (PowerBASIC Console Compiler) bei dem besprochenen Programm primini.exe überflüssig.

Allgemeine Ergänzung zur Pixel-Farbkodierung für Primzahlen

Auf mehrfachen Wunsch dazu eine kurze Zusammenfassung. Alles basiert auf zwei Säulen:

(Prim-) Zahlen mod 30
Jede Zahl, die mod 30 einen der Reste 1,7,11,13,17,19,23 oder 29 ergibt, ist eventuell eine Primzahl.
Anzahl der Farben pro Pixel
Sie schwankt je nach Grafiksystem bezw. je nach Einstellung zwischen
16 = 2^4 ( also Farbe 0 bis 15 ) bezw.
16.777.216 = 2^24 ( Farbe 0 bis 16.777.215 )

Die folgende Tabelle zeigt die Farbenzuordnung von 16 Farben zu den 8 "Primzahlplätzen" von 30 Zahlen.
Es werden 2 Pixel benötigt, gelesen als 2 frei, vorteilhaft definierte Farbwerte für 2 Pixel.
( .... oder gelesen als 1/3 des dualen Farbwertes von 2**24 Farben, siehe unten )

1 7 11 13 17 19 23 29

0     0   0   0   0   0   0   0   0   schwarz
1     1   0   0   0   0   0   0   1
2     0   1   0   0   0   0   1   0   grün dunkel
3     1   1   0   0   0   0   1   1
4     0   0   1   0   0   1   0   0
5     1   0   1   0   0   1   0   1   primes.exe:
6     0   1   1   0   0   1   1   0   0 = teilbar
7     1   1   1   0   0   1   1   1   1 = prim
8     0   0   0   1   1   0   0   0
9     1   0   0   1   1   0   0   1   blau
10     0   1   0   1   1   0   1   0
11     1   1   0   1   1   0   1   1
12     0   0   1   1   1   1   0   0   rot
13     1   0   1   1   1   1   0   1
14     0   1   1   1   1   1   1   0
15     1   1   1   1   1   1   1   1   weiss
------------------------------------

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
1 7 11 13 17 19 23 29 31 37 41 43 47 49 53 59 61 67 71 73 77 79 83 89
0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 nur komplementär!

Die letzten 3 bezw. 4 Zeilen zeigen die ersten 24 möglichen Primzahlen (größer 5) bis zur Zahl 90.
Gelesen als 1 Farbwert für ein Pixel bei 2^24 Farben !!!    verwirklicht bei "primini.exe"   1 Pixel = 1 Text-Zeile)
( oder gelesen als 6 Farbwerte für 6 Pixel bei 2^4 Farben. Diese haben die Einzelwerte:
0000 0000    0000 0100    0000 1000 siehe "primes.exe")
Mit anderen Worten und einfacher, nach freier Definition mit    0 = prim    1 = teilbar ..... :

Die 24 eventuellen Primzahlplätze von 90 Zahlen ( 0 oder 1 ) ergeben direkt
den 24-stelligen dualen Farbwert .... für ein einziges bezw. das erste Pixel des Zahlenverlaufes.

Der Ort des Pixels und seine Farbe liefert für Zahlen >5 "prim oder teilbar".