Ikosaederstumpf = Klassischer Fußball
|
Platonische Körper und Primzahlen? |
Oder Konvexe Vielflächner ... Regular Konvex Solids
Tip: Wenn Sie einen leichteren Einstieg wünschen, gehen Sie bitte nach unten, zum Hexaeder oder Würfel.
Es gibt keine direkte Verbindung zwischen Primzahlen und platonischen Körpern, wenn
man davon absieht, daß beispielsweise die Diagonale einer Würfelfläche die
Seite eines Tetraeders liefert. Die Wurzel aus 2 ist hier im Spiel. Auch die Zahlen der Flächen,
Ecken und Kanten 4, 6, 8, 12, 20, 30 führen nicht recht weiter. Sie sind Vielfache der
3 kleinsten Primzahlen 2, 3 und 5. (Faktoren >5 treten erst
bei höheren Vielflächnern auf.)
Ich möchte Ihnen deshalb meine eigene, ganz andere "platonisch-prime Verknüpfung"
zeigen, die Spaß machen kann, wenn man Zahlen und Formen liebt. Dazu eine fast wahre
Geschichte zum
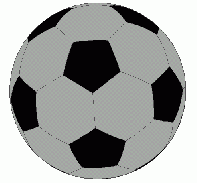
Ikosaederstumpf = Klassischer Fußball

Jemand sagte zu mir, ich solle mehr Sport treiben und weniger am Rechner sitzen. Wie wahr! So sah ich mir denn einen Fußball an (Bild). Dieser Klassiker hat 12 schwarze Fünfecke und 20 weiße Sechsecke. Jeweils 5 der weißen Sechsecke umgeben ein schwarzes Fünfeck. Ich stellte mir die denk-"sportliche" Aufgabe, 20 fortlaufende Primzahlen auf die weißen Felder gezielt zu verteilen. Die Summe der 5 weißen Felder sollte wieder eine Primzahl sein. Nehmen wir an, es sollen die 20 laufenden Primzahlen von 7 bis 83 auf den Ball gesetzt werden, also die Zahlen:
7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83
Die Lösung läßt sich am besten beschreiben, indem
man jene 5 Zahlen in den Spalten einer Tabelle angibt, die ein schwarzes Feld umschließen,
sagen wir mal "links herum". In der untersten Zeile steht die prime Summe. Diese
Art der Beschreibung enthält zwar einige Redundanz, kann aber gut zum Knobeln genutzt
werden. Man kann beliebig beginnen und eine oder mehrere Vorgaben annehmen. Es bleibt spannend
bis zur letzten Zahl!
|
7 |
23 |
17 |
37 |
47 |
61 |
79 |
31 |
41 |
31 |
7 |
11 |
|
61 |
71 |
53 |
83 |
11 |
67 |
43 |
43 |
29 |
41 |
23 |
13 |
|
79 |
59 |
73 |
13 |
67 |
19 |
31 |
19 |
13 |
73 |
17 |
29 |
|
71 |
53 |
83 |
11 |
61 |
43 |
59 |
29 |
83 |
53 |
37 |
19 |
|
23 |
17 |
37 |
47 |
7 |
79 |
71 |
41 |
73 |
59 |
47 |
67 |
|
241 |
223 |
263 |
191 |
193 |
269 |
283 |
163 |
239 |
257 |
131 |
139 |
Bemerkenswert ist bei dieser Lösung, daß es bei keiner
der 12 Summen eine Wiederholung einer Primzahl gibt!
Ikosaederstumpf (wie
oben) Zweite, schwierigere Aufgabe!
Zusätzlich zu den 20 weißen Feldern werden auch die 12 schwarzen
Felder mit Primzahlen belegt, also 32 laufende Primzahlen. Auf der Oberfläche stoßen
an 60 Punkten je 3 Flächen zusammen. Für diese 60 Punkte werden 3er Summen gebildet
mit der Forderung "prim". Daß eine solche Aufgabe nur mit einem Rechner zu
bewältigen ist, bedarf kaum der Erwähnung. Es ist eine Anregung.... Oder lesen Sie einfach im nächsten Abschnitt weiter.
Hexaeder oder Würfel
Täglich begegnen wir diesem bekanntesten Platonischen Gesellen. Er eignet sich hervorragend,
wie alle seine Genossen, zur Kopplung mit Primzahlen. Alle "Regelmäßigen Körper"
haben gemeinsam, daß sie von kongruenten, regelmäßigen Vielecken begrenzt
werden. An den Nahtstellen dieser Vielecke stoßen in der Regel 3 oder 5 von ihnen
zusammen. (Nur beim Oktaeder sind es 4 Dreiecke, die jeweils eine Ecke formen.) Bildet man
die Summe von 3 oder 5 Primzahlen dann erhält man eventuell wieder eine Primzahl,
siehe oben beim Ikosaederstumpf.
Nun sollte man sich auf eine einfache Notation für die Zahlen am Würfel einigen.
Die Abwicklung der 6 Flächen zeigt das linke Bild. Rechts daneben die dafür verwendete,
einfachere (Tabellen-)Schreibweise:
|
Abwicklung
|
Schreibweise für Abwicklung
|
Glücksspielwürfel!
Nicht verwechseln! |
Auf die 6 Würfelflächen sind 6 laufende Primzahlen zu verteilen. Verschiedene Startzahlen für verschiedene Bedingungen.
Eckensummen = prim
Schaut man auf eine der 8 Ecken eines Würfels, sieht man 3 Flächen, bezw. Zahlen.
Die Summe der Zahlen soll prim sein. Es sind somit 8 Bedingungen zu erfüllen. -
In einem überschaubaren Zahlenbereich fand ich insgesamt 6 Lösungen mit folgenden
Startzahlen:
?, 43, 487, 18149, 53527, 53549
Die beiden kleinsten Zahlenreihen sollte man ohne ein Programm in der richtigen Folge finden können. Für 487 lautet die korrekte Notierung:
487, 521, 491, 509, 503, 499
Für die 3 großen Startzahlen wird man wohl ein Programm
benötigen. Interessant ist, daß sich die beiden letzten Primzahlfolgen überlappen:
53527-53593 und 53549-53597.
Tip: Die beiden kleinsten Lösungen haben ein Merkmal gemeinsam.
Legt man den Würfel auf den Tisch, dann hat jeder nur eine Stellung, in der die Summe
der 5 sichtbaren Zahlen keine Primzahl ist.
3 Abwicklungsflächen = prim
Legt man den nächsten Würfel auf eine Platte und kippt 2 mal in die gleiche Richtung,
dann kommen 3 Flächen nacheinander zur Auflage. Die Summe dieser 3 Flächen muß
prim sein. Es gibt nur eine Lösung weit und breit. Finden Sie die richtige Reihenfolge
nach der obigen Notation?
19, 23, 29, 31, 37, 41
!!! Sechser im Primzahl-Lotto !!!
In der Tat, es gibt 6 laufende Primzahlen im Bereich bis 100.000, die es in sich haben. Diese
Zahlen können ohne jede Ordnung auf einen Würfel geschrieben werden. Wie Sie diesen
Würfel auch werfen, die Summe der 5 sichtbaren Würfelflächen ist immer eine
Primzahl!
9733, 9739, 9743, 9749, 9767, 9769
Tetraeder
Der erste in der Reihe der regelmäßigen Körper. 4 Gleichseitige
Dreiecke sind seine Hülle. Setzt man in jede Ecke eines jeden Dreieckes eine Primzahl,
dann benötigt man somit 12 laufende Primzahlen. Als Bedingung gibt man vor:
4 Flächensummen = prim 4 Eckensummen
= prim
Abwicklung des Tetraeders mit einer Lösung
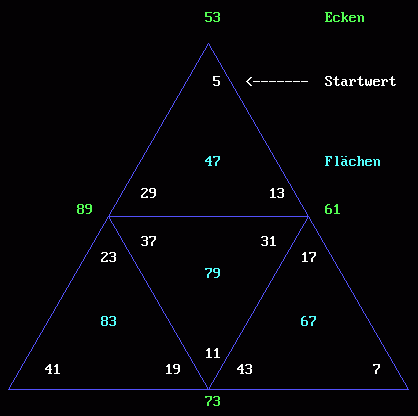
Es gibt viele Lösungen dieser Art. Man kann zusätzliche Bedingungen stellen. In diesem Fall war vorgegeben, die 8 Summen sollten alle verschieden sein, sowohl bei den Flächen, wie auch bei den Ecken!
Viel Spaß bei eigenen Versuchen!