Wenn etwas Freude bereitet, wenn eine Sache Spaß macht, dann sollte man andere Menschen daran teilhaben lassen. Wenn Sie, verehrter Leser, darüber hinaus ein wenig programmieren, dann sind Sie eingeladen.

Mich beeindruckt bei der Perrinfolge und Methode der überzeugend einfache Zusammenhang der (Pseudo-) Primzahlen mit der natürlichen Zahlenfolge. Merkwürdig ist, daß man von dieser Abhängigkeit kaum etwas hört. Dem möchte ich abhelfen und auf drei Fundstellen im Netz aufmerksam machen. - Nebenbei: Pseudoprimzahlen sind die falschen Fufziger, also Zahlen, die nach einem bestimmten Testverfahren prim erscheinen und doch teilbar sind!

Link 1:   Dr. Schmidbauer,  "Perrin pseudoprimes"  http://www.ai.univie.ac.at/perrin.html
Hier erhält man einen ersten Überblick, Tabellen, auch eine Berechnungsmöglichkeit ist gegeben.

Link 2:   Dr. Stephan, "Zahlenfolgen"                        http://www.wias-berlin.de/people/stephan
(Gehen Sie bitte dort zu "personal homepage" und dann zu "Einiges über Zahlenfolgen")
Auf den Seiten 47 bis 49 des Downloads geht es speziell um die Perrin-Folge. Ein Weg zur eigenen Programmierung wird angegeben. Der erweiterte Titel: "Zahlenfolgen bieten den Einstieg in die verschiedensten mathematischen Teildisziplinen." Diese private Homepage könnte auch für Sie zu der Quelle werden. Anschauen!

Link 3:   Dr. Forster, Programm "Aribas"                 http://www.mathematik.uni-muenchen.de/~forster
Der Autor bietet mit Aribas einen Interpreter der Sonderklasse an, noch dazu kostenlos! Das Programm verarbeitet Zahlen mit jeder gewünschten Stellenzahl vor oder nach dem Komma. Jede Rechenoperation, alle allgemeinen Funktionen und viele ganz spezielle Funktionen werden angeboten. Eine herrliche Sammlung von Algorithmen zu Sätzen und Methoden der Zahlentheorie. Ein Muß für einen Zahlennarr!

Die genannten Mathematiker bieten auf hohem Niveau eine "Mathematik zum Mitschreiben" an. Sie sind sich nicht zu schade - insbesondere Dr. Stephan und Dr. Forster - auch einen fertigen Quelltext oder ein Beispiel anzugeben. Das steht sehr im Gegensatz zu den Gepflogenheiten vieler Hochschulen. Dort gilt häufig, je schwerer verständlich ein bekanntes Problem behandelt wird, desto geeigneter ist dann der Text für eine Veröffentlichung. Ich bedauere, so ist es!

Zunächst aber die sehr einfache Definition der rekursiven Folge nach Perrin:
 

n          0 1 2 3 4 5 6 7  8  9 10 11 12 13 14 15 16  17
f(n)       3 0 2 3 2 5 5 7 10 12 17 22 29 39 51 68 90 119
f(n) mod n   0 0 0 2 0 5 0  2  3  7  0  5  0  9  8 10   0

Das ist alles! Mit einem Bleistift und einem Stück Papier kann man sich den einfachen Zusammenhang klar machen oder obige Zahlen weiterführen. Und wie sieht es mit einem kleinen Programm aus? Natürlich ist das schnell geschrieben. Es läuft sofort an ..... und über! Denn das ist die Kehrseite der Medaille. Die Werte für f(n) steigen extrem schnell an. Wollte man z.B. unsere nächste, prime Jahreszahl suchen, also etwa f(2003) überprüfen, dann wäre eine 245stellige Zahl auszuwerten!

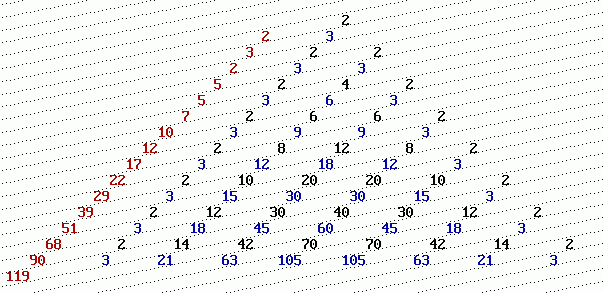
Kleines Zwischenspiel: Untersucht man die Perrin-Folge, dann stößt man schnell auf die Binomialkoeffizienten, siehe auch Link 2 . Mich interessierte nun, wie man die Perrin-Folge in dem PASCALschen Dreieck (PD) ganz praktisch wiederfinden könnte, etwa ähnlich den Fibonacci-Zahlen.... Es gelingt, wenn man zwei PD verwendet, siehe Bild. Das eine PD wird mit 2 erweitert (schwarze Zahlen), das andere PD mit 3 (blaue Zahlen). Die Werte 2 und 3 sind ja die Einstiegswerte in die Perrrin-Folge! Nun werden die beiden Dreiecke ineinander verschoben, bezw. überlagert. Addiert man in schräg angelegten Zeilen, erhält man die f(n) der Perrin-Folge (rot):

Doch zurück zu einer rechnerischen Bearbeitung. Etwas erfahren, wird man die einzelnen Summen  jeweils modulo n ermitteln und bleibt dadurch in einem überschaubaren Zahlenbereich. Dennoch führt auch ein solcher Ansatz nicht zum gewünschten Erfolg. Denn sollte der Perrin-Test für vielstellige Zahlen auf diese Weise durchgeführt werden, dann wäre für jede zu testende Zahl neu hochzuzählen, immer unter Einschaltung von mod n. Auch dieser Weg ist  nicht  befriedigend.

Nun wird's interessant. Um mit hohen Potenzen einer Zahl zu arbeiten, etwa zu prüfen ob diese Potenz modulo m einen bestimmten Wert hat (Fermat-Test), kann das sogenannte "duale Exponentiationsschema" eingesetzt werden. Das ist nicht neu, denn schon vor mehr als 2000 Jahren benutzte man diese Rechenmethode in Indien. Da dieses Verfahren aber allgemein sehr nützlich ist, möchte ich es hier kurz abhandeln.

Zu berechnen sei x^n,   etwa mit x=3 und n=37   also   3^37 ....

• n wird in dualer Form ermittelt ... 100101

• Daraus wird ein Wort gebildet, indem jede 1 und jede 0 ersetzt wird: 1 durch QM und 0 durch Q.  Das Ergebnis ist ...  QMQQQMQQM

• Gestrichen werden die beiden ersten (linken) Buchstaben, das endgültige Wort lautet:  QQQMQQM

• In dem Wort steht Q für Quadrieren und M für Multiplizieren mit x. Ausgehend von x lautet der Wert nach dem jeweiligen Schritt :

x^2  x^4   x^8        x^9          x^18                x^36                                 x^37
9 ... 81 ... 6561 ... 19683 ... 387420489 ... 150094635296999121 ... 450283905890997363  =  3^37

Statt 36 Multiplikationen mit x hat man also nur 7 Rechenoperationen benötigt. Die Zahl der Operationen nimmt mit der Zahlenlänge logarithmisch ab. - Das ist nur ein kleiner Vorgeschmack auf die obigen Links, denn solche und ähnliche Operationen mit raffinierten Vorteilen werden dort verwendet...

Zu Link 2  (Dr. Stephan, ..... Zahlenfolge nach Perrin)
Der Autor verfährt ganz ähnlich und zwar bei einer "effizienten Potenzierung einer dreidimensionalen Matrix". Der Leser sollte sich die Mühe machen und dort nachsehen, es lohnt sich in jedem Falle. Auch die vorangehenden Ausführungen zu Folgen sind sehr wertvoll und verschaffen Einblick in die verschiedensten Zusammenhänge. - Sehr schnell wird der Leser den Wunsch haben, mit größeren Stellenzahlen zu rechnen. Versucht man es mit herkömmlichen Programmen, etwa mit Stringgoperationen in hohe Bereiche vorzustoßen, kann man erfolgreich sein, bleibt aber am unteren, langsamen Ende der Erfolgsleiter. Deshalb....

Zu Link 3  (Dr. Forster, "Multipräzisions-Interpreter Aribas" und "Algorithmische Zahlentheorie")
Mit dieser Software wird jedem interessierten PC-Benutzer ein wunderbares Werkzeug angeboten. Was man immer schon nachvollziehen wollte, mit Aribas gelingt es. Von Fermats "kleinem Satz" - als feste Funktion mit mod n vorhanden - über die Faktorisierung mit elliptischen Kurven bis zu diversen Zahlkörpern der Theorie reicht der Bogen. Mit etwas Programmiererfahrung in Pascal oder C - selbst Basic-Kenntnisse genügen - wird Aribas zur Brücke in die Zahlentheorie.

Als Kostprobe hier ein kurzer Quelltext in Aribas. Er basiert auf Link 2, ist aber etwas verdichtet. Die Funktion "perrin" liefert für r den Wert 0, wenn n prim bezw. pseudoprim ist:

function perrin(n: integer): integer;
external
  r: integer;
var
  a,b,c,i,k,m,u,v,w: integer;
begin
  a:=1; b:=0; c:=0; k:=1;
  i:=n mod 3; m:=n div 3;
  while k+k<m+1 do
    k:=k+k;
  end;
  while k>0 do
    u:=a; v:=b; w:=c;
    a:=u*u mod n + 2*v*w mod n;
    b:=v*v mod n + w*w   mod n + 2*u*v mod n;
    c:=v*v mod n + 2*u*w mod n + 2*v*w mod n;
    if m-k>-1 then
      u:=a; v:=b; w:=c; m:=m-k;
      a:=(u+v) mod n;
      b:=(v+w) mod n;
      c:=(u+b) mod n;
    end;
    k := k div 2;
  end;
  if      i=0 then r:=1;  (* oder: r:=(3*a+2*b) mod n;*)
    elsif i=1 then r:=(3*b+2*c) mod n;
    elsif i=2 then r:=(2*a+2*b+3*c) mod n;
  end;
  return r;
end perrin.

Anmerkung:
An einer anderen Stelle dieser Homepage steht ein 81stelliges Palindrom - prim - der Art  373737373737373...
Mit "perrin" war es ein Kinderspiel das nächst größere zu suchen. Es hat 315 Stellen:  373737373737373737373...

Ich freue mich auf Ihre Mail!