|
Parkettierungen
und Primzahlen ? |
Home |
Eigentlich kann man Parkettierungen und Primzahlen nur begrenzt verbinden. Sicher, es gibt regelmäßige Dreiecke, Vierecke, Fünfecke und natürlich die Sechsecke. Nur zweimal ist die Eckenzahl prim: 3 und 5, wobei das Fünfeck als einziges keine geschlossene Parkettierung erlaubt. Es führt in einem ebenen Parkett immer zu Lücken, die nicht geschlossen werden können.... Es sei denn, man greift z.B. auf das exzellente Penrose-Mosaik zurück, das auf dem Winkel von 72° basiert (5er Teilung). Das einzige Unschöne daran ist, es wurde von einem genialen Denker gefunden - vor den Tagen der Homepages, auch der meinen. Deshalb zum Einstieg in das Thema etwas aus der eigenen Küche, das man so nicht findet....
.... ein "flügges" 5-er Parkett = ein Zehneck mit nur einem Element:

Zurück
zu den Primzahlen: Die 7
wäre die nächste prime
"number",
nach der 5.
Doch 360° durch 7... ? Welch krumme Ziffer! Stellt man
sich zusätzlich die Aufgabe, höchstens
2 Mosaik-Steine anzuwenden - denn bei Penrose gibt
es auch nur den "Drachen" und den "Pfeil" - dann scheint die Sache
hoffnungslos.
Doch hier ist mein (allgemeiner) Vorschlag reduzierbar auf
EINEN Stein:
Ein Siebeneck läßt sich mit Zirkel und Lineal nicht
konstruieren. Aber der Rechner macht
es und legt und dreht das Siebeneck, ganz nach Wunsch:
Was zeigt das Bild?
Auszugehen ist hier von dem blauen regelmäßigen Siebeneck. Dieses wird in 2 Schritten um die rechte untere Ecke gedreht, pro Schritt um einen Winkel von 180°/7. Die 2 neuen Siebenecke erzeugen mehrere Schnittfiguren mit dem blauen Siebeneck. Ich benenne die Figuren:
Links, herausgezogen, hellgrau: Großes (linkes) Dach
Rechts, herausgezogen, dunkelgrau: Großes (rechtes) Dach
Ganz rechts, großes Dach geteilt in: 2x "Kleines Dach" 1x grün, 1x grau = echter Siebeneckabschnitt
Allgemein ist zu sehen, dass eine streifenförmige, periodische Parkettierung (Mosaik) der Zeichenebene in verschiedener Weise mit einem oder zwei Mosaiksteinen möglich ist.
Welche weiteren Möglichkeiten eröffnen die gefundenen Steine? Ist eine 7-fache Anordnung im Winkel möglich? Vorteilhaft verwendet man die 2 grauen Steine "Großes Dach". Diese sind direkt ersetzbar durch je 2x "Kleines Dach". Mit anderen Worten, eine Vielzahl gleicher Steine von einer einzigen Sorte erlaubt eine geschlossene Parkettierung der Ebene (siehe Nachtrag auch für beliebige Winkelteilung n):

Nur zweimal "Ein Streifen Papier" als Meterware würde genügen, um die längeren Abschnitte für den äußeren Kranz zu fabrizieren.... Nun könnte man einwenden, es ist ja eigentlich ein 14-Eck! Kein Problem, das nächtse Bild hat im Zentrum ein lupenreines Siebeneck und die Ringe sind ganz spezielle Polygone. Wieder wurden nur "Große Dächer" verwendet, die durch je 2 "Kleine" ersetzbar sind, siehe den innersten Ring!! Wendet man dies für das ganze Bild an, hat man nur einen Mosaikstein zur Umschließung des Siebeneckes:

Mit dieser
"Segment-Technik" lassen sich
auch Spiralen erzeugen,
siehe unten das linke Bild mit einer 7-er Teilung und....
andere Vielecke mit andern Teilungen n=5, 6, 7, 8, 9... sind
realisierbar. Sie sind
nicht so schön wie die "Penrose Tiles", man kann aber andere Tricks mit
ihnen versuchen.
Das Startbild,
ganz oben, hat nur einen
einzigen Mosaikstein, das "5-er
Dach",
ein echter Abschnitt des Fünfeckes. Das folgende
mittlere Bild zeigt nochmals die vollkommene Harmonie des Musters.
Zusätzlich wurden in den
inneren Ringen die Steine durch Dreiecke ersetzt, um hier den einfachen
Aufbau zu zeigen. Auch
die Flächengleichheit der Mosaiksteine und der Dreiecke wird erkennbar.


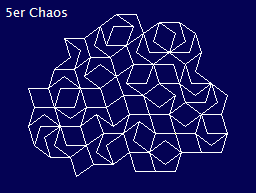
Versuchen Sie im linken Bild das Siebeneck (in der Mitte) zu sehen, als das höchste Siebeneck eines fächerförmig aufgelegten Stapels. Alle anderen Siebenecke liegen sauber ausgerichtet darunter! --- Rechts: Chaos pur, mit 2 Steinen, ein nicht-periodisches Parkett. Das "5-er Dach" mit der zugehörigen "Raute", dem Rest des Ausgangs-Fünfeckes, wie man gut erkennen kann.


Unendlicher
Ausflug:
Stellen wir uns vor, wir belegen mit den aufsteigenden "Vögeln" (2x
5-er Dach) des
kleinen rechten Bildes ein ganzes Fußballfeld oder die Fläche Europas.
Wir befänden uns in
der Mitte dieser endlosen Fläche, wir könnten dann nicht
feststellen, ob wir uns in
einer periodischen Parkettierung befinden oder auch nicht! Irgendwo in
Richtung der noch abzählbaren
Unendlichkeit kann es eine Mitte des linken größeren Bildes geben, wenn
denn jemand die Steinchen
exakt so legt, wie es die Regel verlangt.... Von
allgemeiner Bedeutung ist, daß man bei Steinen, die sowohl ohne
als auch mit Winkeldrehung verlegt werden können, nie sicher sein
kann, ob eine periodische oder aperiodische Parkettierung vorliegt !!!




Oben:
Siebeneck-Parkett,
nur zum Spass als Abwechslung!
Und wie geht es in der Ebene weiter mit dem Siebeneck? Kann man auch
damit unendlich weit füllen?
Antwort im nächsten Bild.
Unten: Dieses Siebeneck-Parkett wurde nur mit einem
7-Eck
konstruiert. Die 7-Ecke liegen teilweise übereinander und
erzeugen so weitere Mosaiksteine,
beginnend in dem Zentrum links unten. Von dort ausgehend wurden
zusätzlich große, gepunktete
Rauten eingetragen. Diese sind eine "Inflation" jener kleinen Raute,
die genau im
Zentrum der gepunkteten liegt. Das Muster der großen Rauten - und somit
die Parkettierung insgesamt
- kann unendlich fortgesetzt werden, immer mit den Steinen der ersten
Raute.

Zurück zu n=5 Nur 1 bis 2 Steine in den
nächsten Bildern...
Zunächst
5er Rauten, als Grundmuster verkleinert: 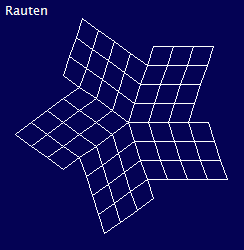
Diese 60 kongruemten Rauten können nun völlig beliebig
gefüllt werden, immer mit der gleichen Anzahl von 'Kleines 5er
Dach' (14x) und Raute' (8x). Als Hilfe können die Linien im
Grundmuster dienen. Das 5er Zentrum (von oben) ist im nächsten Bild
links unten bei der Zahl 213....
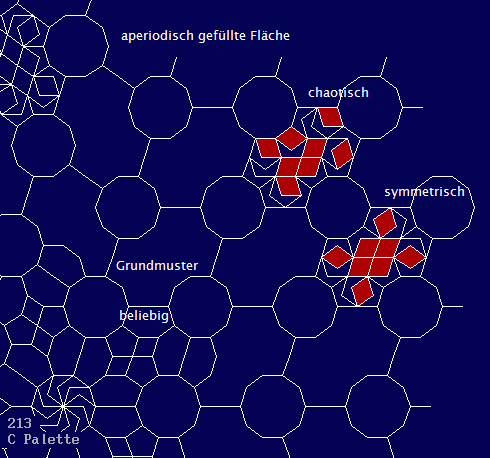
Allg.
gilt für Bilder mit einem
5er Zentrum:
Wählen Sie einen beliebigen Linienzug von der Mitte
an den Rand des Parketts.
Zu diesem Linienzug exakt um 36° bezw.
72° verdreht finden Sie die Wiederholung der
Winkelparkettierung. Das Feld dazwischen
ist beliebig gefüllt mit den 2 Steinen "Dach" und "Raute".
Es sind somit unendlich viele Muster denkbar. Örtliche
Kombinationen können sich wiederholen
und sind - ein nächstes Element dazu genommen - doch wieder
verschieden. In den unteren Bildern sind 'außen' zum Teil
wieder periodische Muster zu finden...
Ähnlich zu den
Penrose-Parkettierungen liefern die beiden Steine (oder auch nur EINER)
eine unendliche
Vielfalt an Mustern, auch Spiralen, Symmetrien, mehr und mehr.
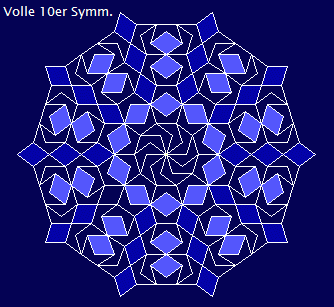



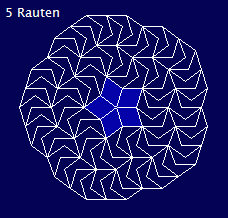
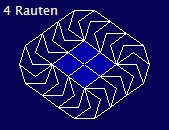
Kleiner Einschub: Ein 'Wurm' - es sind die kleinen 5er Dächer in der Mitte - wurde umkleidet.... Von Zeit zu Zeit werde ich wohl weitere Anregungen anfügen...


|
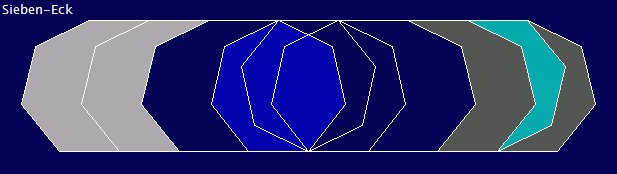
Vergleich von Parkettierungen: |
Penrose, 5-er Teilung |
5-Eck-Segment |
7-Eck-Segment |
|
Goldener Schnitt |
ja |
ja |
nein |
|
Anzahl Elemente |
2 |
1 oder 2 |
1, 2 (3 Spiegelbild) |
|
Besondere Verlegevorschrift |
ja nicht-periodisch |
nein periodisch/nicht-period. |
nein period./nicht-period. |
|
Periodisch füllend mit 1 Element |
nein |
ja |
ja |
|
Winkel-symmetr. füllend mit 1 Element |
nein |
ja |
ja |
|
Winkel-symmetr. füllend mit 2 Element. |
ja |
ja |
ja |
|
Muster zahlenmäßig begrenzt |
ja |
nein |
? |
|
Inflation, selbstähnlich |
ja |
ja |
? |
|
Absolutes Chaos |
nein |
ja, 1 oder 2 Steine |
? |
|
Übergang von Chaos zu Regel |
nein |
ja |
? |
|
Kommentar: |
Exzellent! |
Variabel! |
Nicht erwartet! |
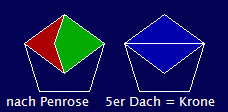
Das linke
untere Bild zeigt ein 5-Eck mit
den 2 Penrose Steinen (rot und
grün). In dieser Anordnung dürfen die beiden nach der Verlegevorschrift
nicht gesetzt
werden. Gleiche Abbildung, daneben: Das zweite 5-Eck umschließt das
"Kleine
Dach"
mit der darüber liegenden geteilten blauen "Raute".
Das rechte untere Bild zeigt die "Inflation"
von 5-er "Kleines Dach"
mit der eingebetteten halben "Raute". Es ist vermutlich die
einzige Lösung einer
selbstähnlichen Abbildung der beiden Steine. Die
Flächenvergrößerung wurde per Programm gesucht
(!). Anschließend erfolgte ein gezieltes Setzen mit der
ermittelten Steinezahl. ( Linearer Faktor = [1+1.618..]*2
= 5.236 )

Nachtrag:
In dem oben genannten
Artikel
"Goldene Schnittmuster"...
http://www.schoenleber.org/penrose/f-d-penrose.html
heißt es:
"In der Theorie bleiben (neben vielen beantworteten) noch einige Fragen offen. Beispielsweise möchte man wissen, ob es Elemente zur nicht-periodischen Parkettierung gibt, die nicht dem Goldenen Schnitt gehorchen. Und ob es nicht vielleicht ein einzelnes Element gibt, das ausschließlich zur nicht-periodischen Parkettierung verwendet werden kann."
Eigentlich gibt mein 7-er "Kleines Dach" auf beide Fragen die richtige Antwort, wenn - wie bei Penrose - eine "Domino-Regel" zugelassen wird. Zusammengefasst gilt für n=7:
Eine Winkelteilung mit n >< 5 folgt - wie gefordert - nicht dem 'Goldenen Schnitt'.
Z.B. füllen die
Elemente der 7-er
Teilung "Kleines Dach" die Ebene lückenlos und nicht-periodisch
dann, wenn einmalig bei der Parkettierung die
Startregel gilt: Die ersten 3 Elemente werden so gelegt, daß
ihre Spitzen in einem Punkt zusammenfallen.
Allgemein: Die Lage der ersten Elemente
bestimmt den Verlauf der Figur. Anschließend geht die Verlegung ohne
eine besondere Regel weiter.

Achtung:
Diese
Parkettierung benötigt nur einen Stein "Kleines Dach"
(dunkelblau, Hintergrund). Wieder wurden 2 dieser Steine zu einem
"Großen Dach" (grau)
zusammengezogen. Die Architektur des Ovals wird so besser durchschaubar.
Und wieder kann man bei einem extrem großen Mosaik örtlich nicht
erkennen, ob eine periodische oder aperiodische Parkettierung
vorliegt !! Ein periodisch erscheinendes Parkett
kann aperiodisch enden !!!
EIN EINZIGER Stein genügt....
wenn man das gleiche Strickmuster
wie für n=7 (oben) für andere n<>7
benutzt :
Das Bild 'Konstrukt
1' zeigt
die prinzipielle Konstruktion aperiodischer Flächendeckungen. Um eine
Kernzelle - hier 6 rote Steine plus 1 grüner
(!) - werden streng tangierend die weiteren Steine (blau) gesetzt. In
die entstandenen Lücken sind in diesem Falle1 bis 3 weitere Steine
einzufügen. Der grüne Stein ist eine erste Erweiterung
des Kernes. Je mehr solcher 'Erweiterungen' verwendet werden, desto
verschiedener die Lösungen (...unendlich viele!). Nebenbei: Statt
des roten Kernes kann natürlich das 10_Eck des allerersten Bildes
dieser Seite treten... Es schließt sich der Kreis.
Am Beispiel der Doppelspirale zeigen die drei Bilder (5,6,8),
daß auch aus dem
Fünf-, Sechs- oder Achteck mit Hilfe des
beschriebenen Steines Dach
eine nichtperiodische
Parkettierung entwickelt werden kann. Die Lage der ersten Steine einer
jeden Farbe bestimmt wesentlich die Figur. Das Prinzip ist
immer
gleich, die ersten Steine 'hängen
quasi ineinander'. Anschließend besteht keine
zwingende Domino-Regel in Bezug auf eine aperiodische
Anordnung.
 n=5
n=5 
 n=6
n=6
(
n=7 siehe oben )
n=8 
 n=9 !!!
n=9 !!!
Am Achteck
(Stein leicht herstellbar, unten) läßt sich sehr gut erkennen,
wann eine Spirale entsteht - und wann nicht !


Und selbst
beliebige Formen sind denkbar. Finden Sie bitte
die kleinste Kernzelle mit 6 Steinen (!) in dem 5er
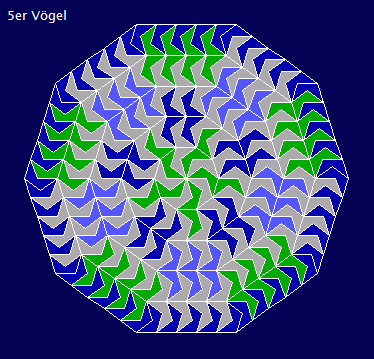
Vogelbauch...

Ich wünsche
viel Spaß bei eigenen Kompositionen.
Aufgelockert ist zu bedenken:
Mit 0 (null) Steinen geht es vermutlich nicht!
Erste Veröffentlichung dieser Art von Parkettierungen in 2001/02.