Im Internet findet man dazu Texte mit Hinweisen auf kluge Köpfe wie Dudeney oder Gardner. Soweit ich erkennen konnte, besteht meist die Vorgabe nur Primzahlen zu verwenden, eventuell so, daß z.B. für ein 4x4 Quadrat 16 laufende Primzahlen zugelassen sind. Auch andere Vorschriften werden diskutiert, aber immer klassisch: Eine "magische" Zahl ist als Summe zu erreichen. Die Zahl muß nicht prim sein.

Mein Vorschlag - auf der Suche nach Neuem - geht in eine andere Richtung. Er ist ganz "primspezifisch" und liegt eigentlich sehr nahe. Es wird nicht eine "magische" Zahl vorgegeben, sondern:

In eine 5x5 Matrix sind 25 laufende Primzahlen so einzutragen,
daß die "magischen" Summen immer eine Primzahl ergeben.

Je länger man sich mit der Geschichte beschäftigt, desto fündiger wird man. Am besten gleich in die Vollen... mit einer der Lösungen:

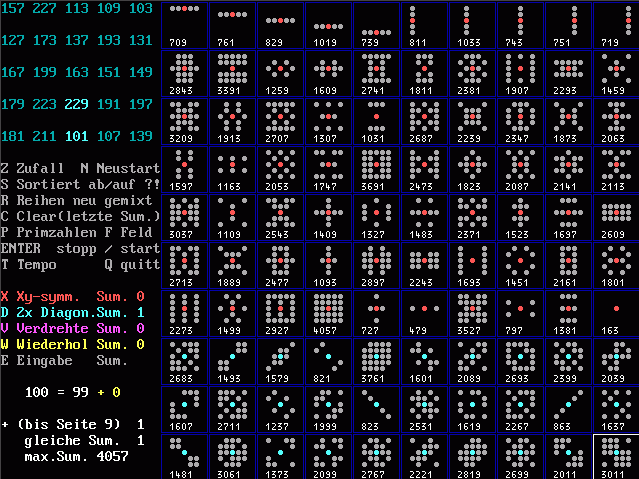
Was zeigen die Felder?

Links oben: Die Matrix 5x5 mit einer gefundenen Verteilung der laufenden Primzahlen von 101 bis 229.
Rechts, großes Feld: Diverse Symmetrien, immer mit dem Feld in der Mitte, denn es muß ja eine ungerade Zahl von Zahlen zu der primen Summe führen. Rot bedeutet Symmetrie zu den Achsen X und/oder Y. Türkis ist dagegen "diagonal-symmetrisch". Alle Zahlenmuster sind prim.
Weitere Schaltungen sind möglich und ergeben immer wieder neue Muster, auch Mehrfachlösungen der gleichen Summe....

Praktischer Nutzen: Null-Komma-Nix, aber schön anzusehen und eine Anregung für eigene Überlegungen.