|
Extrem viele DezimaL-Folgen - einschließlich
der 'einen' Collatz-Folge
|
|
In
dieser Homepage wurde bereits gezeigt, daß es eine ganze Reihe von
Variationen zu der klassischen Collatz-Folge gibt. Die weiteren
Untersuchungen führten zu einem verblüffenden Ergebnis,
das eine
spezielle Seite rechtfertigt, ja sogar verlangt! Was ist zu tun?
Die Collatz-Multiplikation
3*n+1 wird ersetzt durch
y*n+1,
wobei y ausgesuchte Dezimalzahlen sind, mit einer
festgelegten Stellenzahl. Die y Werte liegen nahe (±) der Zahl
3.
(Der Bereich von y=1.000 bis 1.333 (=4/3) ist von besonderer Bedeutung. Siehe unten, letztes Bild.)
- Basislösung:
Das erhaltene Produkt y*n wird aufgerundet zur nächsten geraden Zahl !!
Für y=3.00 ändert sich somit nichts gegenüber der
Originalfolge nach Collatz 3*n+1 .
Die
Möglichkeiten eines Compilers zur Auf- oder Abrundung von
Zahlen
sind vielfältig. Das kann man ausnutzen, um völlig
unterschiedliche Dezimal-Folgen zu erzeugen. Zunächst werden zwei Arten von Folgen betrachtet, alternativ mit Auf- oder Abrundung, jede
mit einem anderen Zahlenverlauf.
(Man könnte auch eine beliebige Rundungsgrenze wählen... für die letzte Stelle 2, 5 oder 7...)
Jede dieser Vorgaben erschließt ungezählte, neue
Dezimal-Folgen, deren Verlauf exakt der Collatz-Vermutung entspricht:
Sie sind 'fallweise schleifenfrei', je nach gewähltem y. Man muß
erkennen, auch die klassische Collatz-Folge 3n+1 (...Aufrundung) ist nur 'fallweise
schleifenfrei', gegenüber der Folge 3n-1, was einer Abrundung entspricht.
Der einzige Unterschied zwischen
Collatz und den Dezimal-Folgen y*n(±1) ist:
Die
Glieder der Y-Folgen herab bis zu
1 sind ungleich
den gewohnten Collatz-Zahlen.
Man wird die Sache natürlich per Rechner
angehen, insbesondere um
eine exakte
Rundung der Dezimalstellen zu sichern. Eventuell
sortiert man einmalig jene y Werte aus, die zu einer
Schleifenbildung führen. Besser: Man fährt 'online' und
unterdrückt
die kritischen y Werte, die zu Schleifen führen.
Als
Demonstration dient das nächste Bild, mit AUF-Rundung, türkis markiert.
Achtung: Hier werden nur die ungeraden Folgenglieder (als Kurznotation) ausgegeben !
Es wurden dreistellige y
Werte gewählt, die primfallbedingt
keine
Schleifenbildung erzeugen...
y=3.190 bis 3.200. Für jede beliebige Startzahl findet man
interessante
Folgenlängen.
Sie sind zum Teil gleich lang und führen über jeweils andere Glieder zu EINS
!!
Es
bedeuten bei ikm ...
i Anzahl Glieder der Normalfolge
m Anzahl Multiplikationen
k Anzahl Glieder der gekürzten Folge = Anzahl
der Divisionen (hier nicht dargestellt)

Wie sehen dagegen direkt
benachbarte y-Dezimal-Folgen
zu kleinen
Startzahlen aus?
Wir wählen dazu 3-stellige Dezimalzahlen y nahe 3
Bereich... y=3.000 ±0.005
Das verwendete Programm liefert: 11 verschiedene, sehr ähnliche
Folgen für n = 27.
Sie sind verschieden lang, schleifenfrei und enden alle bei
EINS.
Dreimal treten die Originalwerte von Collatz auf, bei
y=2.999, y=3.000
und y=3.003
Die
Ergebnisse sind abhängig von den Primfaktoren der durchlaufenen Zahlen,
genau so, wie es für die Original-Collatzfolge mit
3*n+1
in dieser Homepage angegeben wurde. Zur Erinnerung:
/ Der Folgenverlauf für jede (ungerade) Zahl n wird bestimmt durch die Primfaktoren von n+1. /
Dazu nächstes Bild:
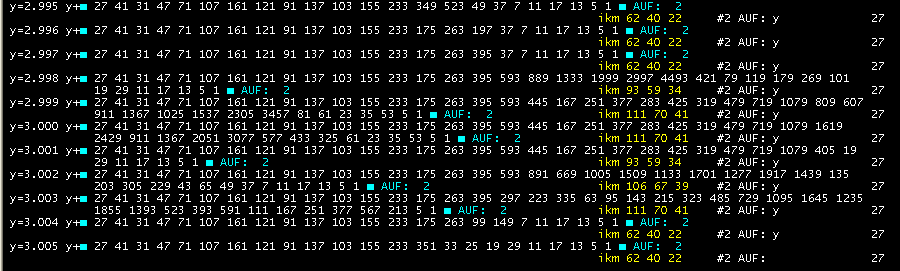
Den Unterschied zwischen y=3.000 und y=2.984 bei n=27 kann man gut erkennen.
Nur die ersten 5 ungeraden Folgenwerte 27,41,31,47,71 sind gleich:

Ohne Benutzung des Wortes 'Beweis' wird damit gezeigt, daß der
Collatz-Algorithmus als eine
primfallbedingte
Zufälligkeit, innerhalb
von Folgen der Art y*n(+1), anzusehen ist.
• Die Primfaktoren von y*n±1 sind für den
Folgenverlauf entscheidend... = 'primfallbedingt' !!
Wie bei Collatz bestimmen diese geraden / ungeraden Primfaktoren das nächste Folgenglied.
• Collatz... 3n+1 ist schleifenfrei •
3n-1 (...entspricht einer Abrundung) dagegen nicht!!
Wichtig:
Sollten Sie versuchen, die gezeigten Folgen mit einem eigenen
Programm zu erzeugen, könnten Sie eventuell andere
Glieder zwischen n und 1 erhalten. Das ist absolut kein
Fehler,
sondern nur eine Bestätigung der geschilderten Situation. Im Gegenteil:
Welche
Art der
Zahlenrundung auch verwendet wird, das Ende bei 1 ist
davon
unabhängig, es ist immer gesichert - geprüfte Schleifenfreiheit
vorausgesetzt.
Damit verändert sich
das gesamte Bild der Collatz-Vermutung mit dem Folgenende bei EINS !!
Wählt
man Startzahlen in hohen Bereichen - mit mehreren
Dezimalstellen für den Wert y - findet man
extrem viele Dezimal-Folgen. Sie sind sehr ähnlich und
doch vollkommen verschieden zu Collatz.
Die
'primfallbedingte'
3n+1 Folge hat das Alleinstellungsmerkmal
verloren. Sie ist eine
schleifenfreie Folge von sehr vielen, die alle bei EINS enden.
Bisher wurde nur diese eine Lösung - nach Lothar
Collatz - tausendfach untersucht.
Ein direkter
Beweis zu der einen
Collatz-Folge kann mit den neuen Erkenntnissen nicht geführt werden. Jedoch:
Es läßt sich an Hand extrem vieler nun vorliegender Y-Folgen zeigen:
- Es
gibt ungezählte Folgen (ohne und mit Schleifen) vergleichbar mit Collatz
bzw. mit 3n±1 .
- Für y=1 bis y<=4/3 sind 'auf- und abgerundete' Folgen immer schleifenfrei.
- Für y>4/3 bis y<10/3 sind die 'auf-oder abgerundeten' Folgen - 'primfallbedingt' - schleifenfrei.
Sehr oft steht einer abgerundeten, nicht schleifenfreien Folge
eine aufgerundete, schleifenfreie Folge entgegen. Zwingend ist
dieses Verhalten jedoch nicht.
- Folgen
mit Endlosschleifen können bereits im niederen Zahlenbereich
sicher erkannt werden.
Suchläufe bis in höchste Stellenzahlen, wie man es in den letzten
Jahrzehnten bei Collatz durchführte, sind nicht notwendig. Die Prüfung
einiger hundert oder tausend niedriger Startzahlen genügt, um
einen
schleifenfreien y Wert sicher zu
ermitteln.
Frage: Was
bewirkt eigentlich das gebrochene y<>3 ?
Durch die spezielle Multiplikation [y*n(±1)] wählt
man auf der
Zahlengeraden einen
etwas höheren oder niedrigeren Einstiegspunkt für die nächste
2er-Divisionen... höher oder niedriger gegenüber Collatz mit y=3. - Im
weiteren Verlauf zeigt sich, ob 'primfallbedingt'
eine schleifenfreie Folge entsteht. Die Sache ist beschämend einfach und
doch korrekt und gleichwertig zu Collatz. Vermutlich wird man das y-Konstrukt ablehnen, langfristig jedoch ohne
Erfolg.
Alle bisherigen
Aussagen zu Collatz 3n+1 gelten prinzipiell auch für y-Folgen, z.B.:
- Alle
Y-Folgen sind in ihrem Verlauf (Länge) ebenso wenig voraus berechenbar
wie die Collatz-Folgen. Denn: Ausgehend von einem Startwert n wird
jedes nächste ungerade Glied n' nur bestimmt durch den Faktor y
(1 bis ~3) und die Primfaktoren von n±1 (Auf- Abrundung).
- Zum
Thema Permutation: Die in dieser Homepage vorgestellten Zusammenhänge von (Collatz-)
Basisfolgen 2^n und den Collatz-Folgen selbst gelten ohne Einschränkung für
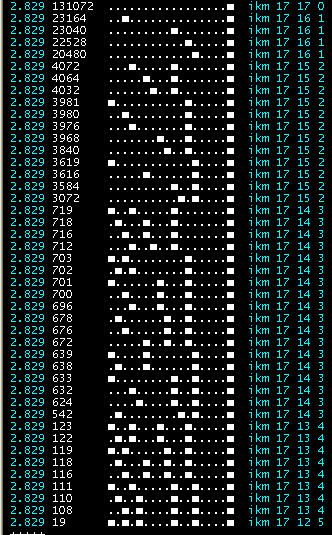
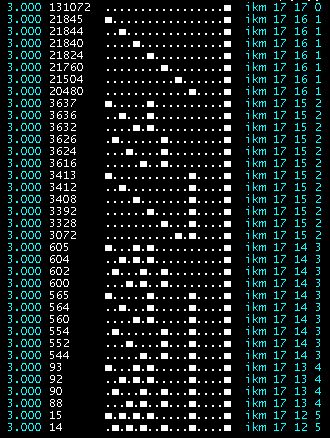
die schleifenfreien Y-Folgen. Als Demo hierzu dient die wahlweise Permutation der Basisfolge 2^17 =
131072 :
für
y*n(+1) y=2.829
...zum Vergleich für Collatz
3*n+1
- örtlich
gehäuftes Vorkommen von Folgen mit gleich vielen
Multiplikationen:
| Obere
Schranke, statt s = 2^i \ 6^m
neu... s ~ 2^i \ (2*y)^m |
- kein
Überwiegen von Multiplikationen innerhalb einer gegebenen
Folgenlänge i
- primfallbedingt
auftretende Schleifen, sehr ähnlich der Folge 3n-1
Nochmal und NEU:
Die bisher vorgestellten Fakten sind auf die
neuen ungezählten y-Dezimal-Folgen übertragbar.
Man
kommt zu dem Schluss: Es sind unendlich viele Y-Folgen möglich... bei
'unendlich' vielen Dezimalstellen in extrem hohen Bereichen.
Es ist interessant und es ist noch genügend zu tun. Ich freue mich über jede Mitarbeit.
Hier eine Eingabe für n von 12x der Ziffer 7. Selbsterklärend
öffnet sich eine Vorschau in beliebig hohe Bereiche...
immer
herunterführend zur konstanten EINS.
y=2.89834 aufsteigend (letzte Stelle)
n=777777777777 konstant (12
Stellen)

17.8.2011 •
Programmtechnisch ist noch mehr zu erwarten. Bitte verfolgen
Sie diese Seite.
11.11.11
•
Kein Faschingscherz, sondern ein Programm zu den neuen
Y-Dezimalfolgen
Download:
Collatz-w.zip ( bitte gelegentlich erneuern, wird noch erweitert )
Das Programm gestattet ein Studium verschiedener y-Werte.
Welche sind schleifenfrei ?
Zum Einstieg genügen die Steuertasten W, S oder
YY, XX , siehe die dortigen Tipps.
DEMO zu 'aufgerundet', erstellt mit Collatz-w.exe:
Wählt man nur eine Dezimalstelle, hat man bereits 7 Alternativen zu
y=3.0, n=27 .

Bei zwei Stellen ist die Auswahl weit größer, gültig für jedes
beliebige n (hier n=1001)
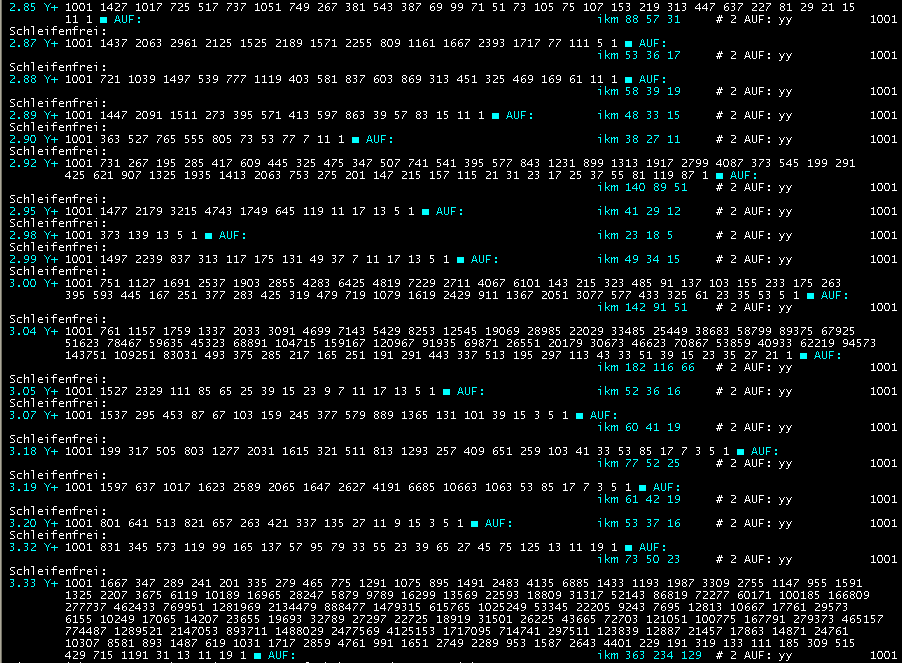
Nicht berücksichtigt ist im letzten Bild der Sonderfall der 2x 33 Folgen von y=1.00 bis y=1.33 (4/3).
Es sind 66 Folgen, da genau dort - und nur dort - auch die 'abgerundeten' Werte schleifenfrei sind.
Mit ein wenig Knobelei erkennen Sie den Hintergrund!
Das nächste Bild zeigt daher an wenigen Folgen jeweils in zwei Zeilen die auf- und abgerundeten Werte für ein n. Total wären es 666 verschiedene Y-Folgen , jede für unendlich viele n. Alle Folgen sind schleifenfrei, exakt nach der Collatz-Vermutung mit dem zwingenden Ende bei EINS.
Der Grund für dieses spezielle Verhalten ist sehr einfach:
Für alle y=1 bis y<=1.333 (4/3) ist jedes ungerade Folgenglied n' kleiner als sein Vorgänger n.
Das gilt für jede Auf- oder Abrundung, eine Schleifenbildung kann hier nicht entstehen.

Viel Vergnügen bei der neuen Sicht auf die alte, entkleidete
Collatz-Vermutung mit y=3 !!









